Index of /kankel/ph262/filters

[ICO]NameLast modifiedSizeDescription
[PARENTDIR]Parent Directory  -  
[DIR]recipes/2012-02-07 02:27 -  
[DIR]dB/2012-02-07 02:26 -  
[DIR]calculations/2012-02-07 02:27 -  
High Order Filters

High Order Filters

Outline

  1. Review Relevant Concepts
  2. High Order Filter Recipes
  3. Butterworth, Bessel, and Chebyshev Filters
  4. The Ideal Filter

Review Relevant Concepts

Bode Plots

As usual, we will plot gain (dB) and phase (degrees) as a function of log frequency (Hz).

Remember that angular frequency (radians/s) is 6.28 times larger than the frequency in Hz.

Cascaded Filters

We found that an nth-order filter could be constructed by cascading n first order flters.

We get sharper response, and keep the math simple, if we buffer between filters to prevent loading issues. The transfer function of the whole thing is then the product of the transfer functions of all the individual stages.

Cascaded LC filters have a soft knee that cannot be overcome by any amount of cascading.

2nd Order Filters

A series RLC filter makes a fine 2nd orer high pass or low pass filter. We discussed some disadvantages with inductors, including noise susceptibility, parasitics, and (particularly at low frequencies) size, weight and cost.

Active filters, such as the Sallen-Key, allow us to produce a general second-order filter with buffered output from 2 resistors, 2 capacitors, and one op amp. No inductors are needed. Provided that we want to cascade them, the op amp would be necessary anyway. So active filters are widely used.

The general response of a 2nd order low pass filter stage is:

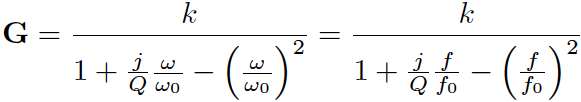
Q: What are the corresponding formulae for 2nd order high pass and bandpass filters?

We quantified 2nd order filter response with Bode plots, time delay and response to steps and impulses. The gain k is only a constant multiple, but remember that the variant of Sallen-Key we have studied uses two identical resistors with two identical capacitors; so k is used to adjust the quality factor Q. The remaining parameter is the natural frequency, which depends on component values.

High Order Filter Recipes

The 2nd order active filter is a powerful tool for cascading. Often, each stage will have a different natural frequency and Q.

Critical Frequency

In last week's homework, you derived formulae relating natural frequency (the quantity f0 in the response function, which we can easily relate to component values) to critical frequency (usually defined as the -3dB point) for high pass and low pass second order filters. Now look at my note at the end of the solution (alas, I see that I confused fn with 1/fn). More generally, when we design a multi-stage filter, the natural frequency of each stage is tuned differently to achieve a combined effect. These scale in proportion to the critical frequency of the filter as a whole. Horowitz calls this proportionality constant fn. Therefore, two parameters are listed for each stage:

There are tables, charts, and even whole books full of famous filter recipes. Almost any desired frequency response can be constructed by a suitable combination of 2nd order stages, optimizing the two parameters for each stage. This results in a filter with an even number of poles, by which we mean a polynomial of even order in f in the denominator of the response function.

Filters with an odd number of poles can be constructed by adding a buffered RC filter stage, but like Horowitz I consider this a waste of a good op amp.

Butterworth, Bessel, and Chebyshev Filters

We will now discuss three popular types of multistage filter recipes. Each is distinguished by a particular figure of merit for which the filter parameters have been optimized.

Bandpass filters are constructed by cascading a multistage high pass with a multistage low pass. There are thus two distinct critical frequencies; these edges define the passband.

Butterworth

The Butterworth filter is designed to have a flat response in the passband and a sharp knee.

Bessel

The Bessel filter has a flat time delay within the passband.

Chebyshev

The idea behind the Chebyshev filter is that, if we are willing to accept some passband ripple, the knee (edge, corner) can be made sharper. A family of Chebyshev filters is specified by the size of the envelope, in dB, for allowed ripples in the passband. Horowitz tabulates parameters for 0.5dB and 2dB ripple. A much broader variety have been tabulated elsewhere.

Summary Plots

We conclude by comparing plots of various filter types with 8 poles.

Questions to ponder:

  1. How would you design a high pass filter that minimizes the distortion of waveforms with frequency greater than 1 kHz, but suppresses frequencies below 100 Hz by at least 30dB?
  2. How would you design a Chebyshev bandpass filter with 6th order roll-off on each side of a passband from 10-20 kHz? What components would be required?
  3. Is it possible to use the same method to produce a bandstop (notch) filter? If not, can you think of another way to do this?

Aside: The Ideal Filter

What is the ideal filter? According to some engineering texts, it is the Brick Wall.

Questions to ponder:

  1. In what sense is the Brick Wall ideal? What is it good for? What is it not good for?
  2. The impulse response of the Brick Wall is centered on the impulse, and the ringing dies off slowly like 1/t in both directions. What does causality imply about the time delay associated with such a filter?
  3. Can a Brick Wall be approximated with analog components? Can it be built at all?