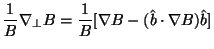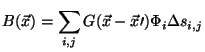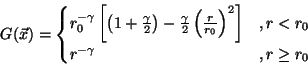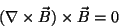
Force-Free Fields
As magnetic flux tubes rise up through the convection zone of the sun and reach
the surface, they quickly expand into the low density of the solar corona. When
this occurs, two prominent regions are created: one with positive magnetic
flux through the photosphere, and one with negative flux. The corona is composed
of a low-beta plasma, in which the magnetic pressure is much greater than the gas
pressure. Therefore, the magnetic stress is
balanced only by the repulsion it experiences from the gradient of other neighboring
fields and the
magnetic images created below the photosphere. These conditions are generally referred
to as magnetohydrostatics (MHS), and this type of force-free
magnetic field and is governed the Lorentz equation:
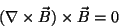
Although the equations of magnetohydrodynamics reduce to this simplified form, the solutions are still quite complicated. In 1990, Low and Lou proposed a limited set of nonlinear solutions to this rather complicated equation. The use of their solution set effectively generates the magnitude and direction of the magnetic field at any point in the space z>0.
The Fluxon Model
A "fluxon" is simply an area of constant magnetic flux. In this
model, each fluxon is represented simply by a line that runs through
the center of the flux bundle. To accomplish this, a
line-of-sight magnetogram (as generated by the Low and Lou equatios) is divided up into
small squares of constant positive flux and a dot is placed in each square,
which represents the starting points for each fluxon.
The above Lorentz equation can be used, in combination with some
vector identities, to derive the following form of the force-free field equation that was our main
focus:
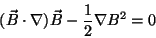
This equation can then be separated into a more explicit expression of the magnetic field direction and magnitude as follows:
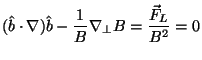
In this form, it is more obvious that the first term is the amount of curvature of a circle locally tangent to a segment of a specific magnetic field line. The second term is, of course, the perpendicular gradient of the spacing of flux lines. The combination of these two interpretations shows that the Lorentz Force is always directed perpendicular to the field lines. Furthermore, the first term can be said to represent the tension of the field lines, while the second term represents the outward pressure gradient of the field. In order to further understand this concept, consider the more simplified model of a fluxon as a short, relatively straight flux tube that is constantly seeking to minimize its energy. Since we are primarily concerned with magnetic interactions and properties, the total energy is given by the fluxon's magnetic energy.
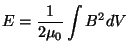
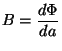
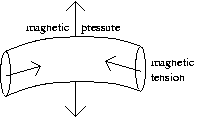
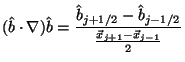
where j is a point along a specific field line (i), and the magnetic field directions are calculated by the following method.
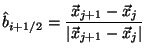
Next, the magnetic pressure gradient must be calculated. To do this, it is best to rewrite this term as