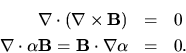Next: About this document ...
Notes on Plasma 
R. McMullen 02/21/02
One foundation of hydrodynamics is the Navier-Stokes Equation, a specific form of the equation of motion (or inertia) for a viscous fluid. A good derivation can be found in The Physics of Fluids and Plasmas by Arnab Choudhuri, chapter 3. (In fact, the following borrows heavily from ch. 14.)
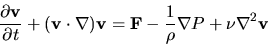 |
(1) |
The 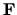 can be gravity, or a rotational force, or magnetic force, whatever force is felt by the body of the the fluid (or gas) being considered. This then is the place where we stick in the Lorenz Force,
can be gravity, or a rotational force, or magnetic force, whatever force is felt by the body of the the fluid (or gas) being considered. This then is the place where we stick in the Lorenz Force,
In an ionized gas, the Lorenz Force will act separately on electrons and ions
One of the fundamental assumptions of plasma physics is charge neutrality - that the charges balance:
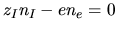 . One more thing, define the drift velocity
. One more thing, define the drift velocity
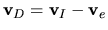 . Then
. Then
Now use Ampére's Law:
where the current is defined as
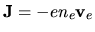 , and neglect the
, and neglect the 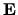 term (OK as long as
term (OK as long as
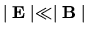 in the Corona). Then the force becomes
in the Corona). Then the force becomes
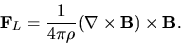 |
(2) |
With this substitution, we write the Navier-Stoke's equation in its 'familiar' form, used for MHD (Magneto HydroDynamics, the study of magnetized fluids).
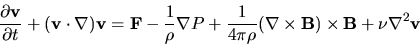 |
(3) |
This equation is solvable numerically for specific geometries and boundary conditions, when coupled with the rest of the MHD equations. For starters, though, we do as much as we can analytically. One obvious starting point is to set 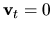 , but we'll go even farther and set v = 0 as well. While we're at it, neglect any other body forces (
, but we'll go even farther and set v = 0 as well. While we're at it, neglect any other body forces (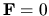 ). Notice that the mass density dependence in
). Notice that the mass density dependence in  drops out.
drops out.
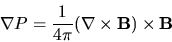 |
(4) |
Solutions to Equation 4 are know as Pressure Balanced Fields because the forces from the magnetic fields are balanced by the pressure. This is still not trivial! It helps shed some light to break up the RHS ala the front cover of Jackson, which gives us a magnetic pressure term and a magnetic tension
BEGIN ASIDE
The magnetic forces on the RHS are still mysterious, so we split it up farther:
where
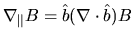 , etc. Applying the chain rule and reducing where posible, we find:
, etc. Applying the chain rule and reducing where posible, we find:
Things to notice: 1) the magnetic pressure term (
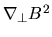 ) acts only perpendicular to the direction of the field unlike a pressure gradient, which has no preferred direction. 2) The term
) acts only perpendicular to the direction of the field unlike a pressure gradient, which has no preferred direction. 2) The term
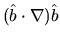 is a curvature term which always points to the center of the arc for which it was evaluated.
is a curvature term which always points to the center of the arc for which it was evaluated.
END ASIDE.
Returning to the pressure balanced field equation, we find
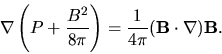 |
(5) |
This equation says that the plasma will exhibit very different behavior in gas-pressure dominated conditions vs. magnetic pressure dominated conditions. How do we know which of the combined pressures will dominate? The plasma parameter 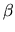 , the ratio of the pressures, can help us think about this.
, the ratio of the pressures, can help us think about this.
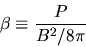 |
(6) |
In regions where the gas pressure is much greater then the magnetic pressure, the magnetic tension will be balanced by the gas pressure.
Likewise, where the magnetic pressure dominates, the magnetic forces alone will balance.
This last we can write equivalently as the Force Free Field equation for low 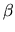 , which was canonized in 1954 by Lüst and Schlüter,
, which was canonized in 1954 by Lüst and Schlüter,
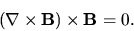 |
(7) |
Solutions to Equation 7 are quite prevalent in the state of the art of magnetic field extrapolations. In general, its solutions can be broken into two classes, linear and nonlinear force free fields.
Essentially, Equation 7 requires that the magnetic field is parallel to its own curl, so can define 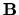 in terms of it's curl and an unspecified scalar function
in terms of it's curl and an unspecified scalar function 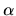
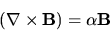 |
(8) |
Note that (Equation 8)
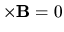 for all
for all 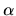 and
and 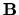 .
We can begin to constrain
.
We can begin to constrain 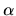 by taking the divergence of
by taking the divergence of
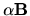 (using the chain rule and
(using the chain rule and
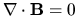 )
)
Whatever the functional form of 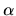 , it can't vary along
, it can't vary along 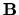 , only perpendicular to
, only perpendicular to 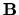 . If we choose
. If we choose 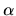 to be a constant, then Equation 8 is linear and can be solved as a series expansion. Its solutions are known as Linear Force Free Field extrapolations. If
to be a constant, then Equation 8 is linear and can be solved as a series expansion. Its solutions are known as Linear Force Free Field extrapolations. If 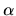 is allowed to vary perpendicular to
is allowed to vary perpendicular to 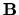 , then Equation 8 is nonlinear, with solutions known as Nonlinear Force Free Field extrapolations.
, then Equation 8 is nonlinear, with solutions known as Nonlinear Force Free Field extrapolations.



Next: About this document ...
Rebecca McMullen
2002-02-25
![]()
![]() , but we'll go even farther and set v = 0 as well. While we're at it, neglect any other body forces (
, but we'll go even farther and set v = 0 as well. While we're at it, neglect any other body forces (![]() ). Notice that the mass density dependence in
). Notice that the mass density dependence in ![]() drops out.
drops out.
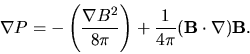
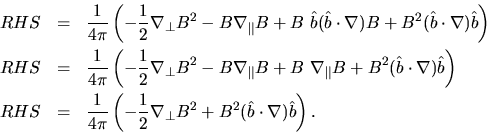
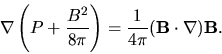
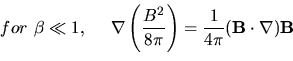
![]() in terms of it's curl and an unspecified scalar function
in terms of it's curl and an unspecified scalar function ![]()