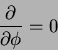
Previous  Presentation Outline  Next
Our Dynamo Model

Assuming Axisymmetry, which means basically that

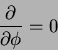
\begin{displaymath}{\partial \over\partial \phi}=0\end{displaymath}

The magnetic can be written as:
 
 

\begin{displaymath}{\bf B}=B(r,\theta,t){\bf e}_{\phi}+\nabla\times{[A(r,\theta,t){\bf e}_{\phi}]}\end{displaymath}

and the velocity field can be written as:
 
 

\begin{displaymath}{\bf v}={\bf v}_{p}(r,\theta){\bf e}_{\phi}+r\sin(\theta)\Omega(r,\theta){\bf e}_{\phi}\end{displaymath}







If we introduce this in the induction equation
 
 

\begin{displaymath}{\partial {\bf B}\over\partial t}=\nabla \times ({\bf v\times B })+ \lambda \nabla^2 {\bf B}\end{displaymath}

We obtain the next two equations:
 
 

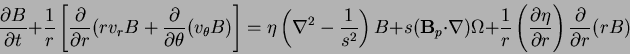
\begin{displaymath}{\partial B\over\partial t}+{1\over r}\left[{\partial \over\......tial\eta \over\partial r}\right){\partial \over\partial r}(rB)\end{displaymath}





for the toroidal field and

\begin{displaymath}{\partial A\over\partial t}+{1\over s}({\bf v}_{p}\cdot\nabla)(sA)=\eta\left(\nabla^2-{1\over s^2}\right) A +Q\end{displaymath}






for the poloidal field where \begin{displaymath}s=r\sin\theta\end{displaymath},\begin{displaymath}Q=\alpha B\end{displaymath}

To see a movie of one of our simulations with solar-like behavior  click here
 
 

The parameters we will study are:

\begin{displaymath}v_{0}\end{displaymath}             the magnitude of the meridional flow.
\begin{displaymath}\alpha_{0}\end{displaymath}              the proportionality constant in the source term for the poloidal field.
\begin{displaymath}\eta_{0}\end{displaymath}               the diffusivity of the magnetic field.
\begin{displaymath}\Delta\Omega\end{displaymath}          the shear in the differential rotation.
 
 
 
 Home