The Inscrutable DEM

Science Nugget: March 31, 2000

Frontispiece

The image below shows a composite soft X-ray difference image (dimming on the W limb) and coronal mass ejection (both limbs) from a major flare that happened on the invisible hemisphere during the depths of solar minimum, 1996. It has nothing much to do with the subject of this science nugget, but every nugget should have a pretty picture - this one is courtesy L. W. Acton. The square in the middle shows an X-ray difference image - the dark patch at the west limb is a nice example of coronal dimming - and the surrounding image is an optical one from the LASCO coronagraphs on SOHO.

The coronal images shown above give us a view of coronal magnetic restructuring during a mass ejection, but normally the structure remains stable. During these quiet times the force of gravity imposes a hydrostatic equilibrium on the coronal matter, and we often make the assumption of spherical symmetry as a model with which to interpret the observations. Probably this frontispiece will make the reader suspicious about this assumption, but it's the "zeroth approximation" to the truth and the one that we adopt in the discussion below. Actually, the frontispiece above shows difference images, which accentuate the changes, so the approximation really may not be that bad.

We interpret the image as follows: a flare occurred far around on the invisible hemisphere; it resulted in X-ray dimming visible as the dark area on the inset SXT image at the W limb. This showed the origin of some of the CME material that came spewing out, as shown in the outer (LASCO) image. The X-ray image shows brightenings both north and south, suggesting that the overall restructuring dropped energy into these quadrupolar features. Somebody should write a paper about this image!

Background

A plasma, such as the material of the solar corona, emits radiation when ions and electrons collide - normally one quantum (photon) per collision. The brightness of a given feature in the X-ray spectrum thus must be proportional to the electron density ne and to the density of the emitting ion ni. It also scales as the total volume V of the emitting plasma, of course, so the total brightness should scale as nineV. This is the emission measure. Because the ion density can depend upon temperature, we normally have to reckon on emission measure as a differential quantitity, i.e. a function of temperature. This is what is called "differential emission measure," or DEM,

y(T) = d(nineV)/dT.

Basically observations tell us the emission measure, and the we infer local physical parameters such as density and pressure.

Solar physicists spend much happy time debating about the relevance of DEM, as opposed to the simpler assumption that everything is isothermal. This latter is usually not as stupid an approximation as it sounds, but of course in principle it is always wrong. But how wrong? This nugget describes a well-controlled theoretical situation where we know that the source is multi-thermal, and what its geometry is. Let us use this example to see how much it would change our naive intepretation of the Yohkoh SXT observations.

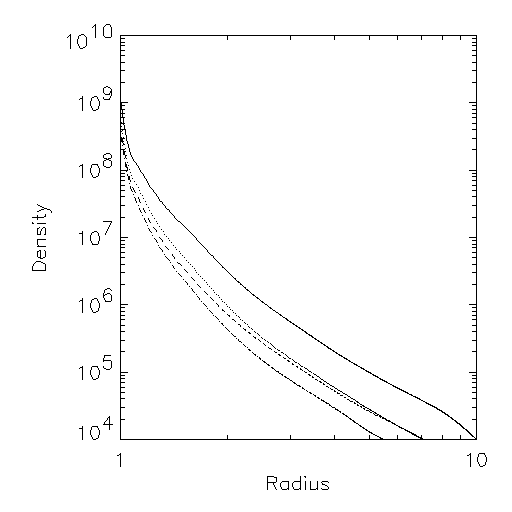
Withbroe's models of the corona and solar wind

Although better models probably exist by now, a 1988 paper by G. Withbroe gives us some representations of the corona with which to model the X-ray emission. We need the variation of density and temperature with radial distance, basically, and from this we can integrate to obtain the projected coronal brightness. We need to do this integration because the corona is optically thin (transparent). At the very limb we will anticipate a jump by exactly a factor of two for a spherically-symmetric corona. These are the models, density on the left, and temperature on the right:
Withbroe models in decreasing order of peak temperature:

  • "Quiet corona"
  • "Polar coronal hole, maximum"
  • "Equatorial coronal hole"
  • "Polar coronal hole, minimum"

    • Withbroe built these models up from a wide variety of data, obtaining a synthesis for each of four representative conditions. The "coronal hole" models represent the naked corona of the solar wind, which he modeled differently for solar maximum and solar minimum activity. These models no doubt suffer from the fate of all such models, gradually becoming obsolete as data improve (for example, what do Yohkoh data contributet?). But they will serve well just to illustrate the DEM problem.

    What should SXT see?

    The answer to this question depends upon the SXT spectral response, some atomic physics, and some plasma physics. The latter tells us what ions should be present at a given temperature; the atomic physics tells us how bright their emission lines and continua should be; and the SXT spectral response folds this information into an integral over wavelength to give signal (per unit emission measure) as a function of temperature. Integrating this over the DEM then gives the total signal - very simple, but clearly a calculation involving several possible pitfalls.

    First, the DEM itself: This is a function of the impact parameter of the line of sight through the corona. Impact parameter zero would be an integration straight into the geometric center of the Sun; unity would be just tangent at the limb; a value 1.5 would have a projected height of half a solar radius above the photosphere. Here are these three cases:

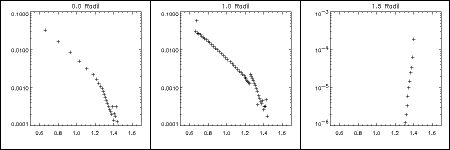
    These DEM's clearly have distributions in temperature (the X-axis, in units of millions of K), so we would expect the SXT response to differ from (say) the isothermal model evaluated at the projected height (for impact parameter > 1); for a view straight down at disk center, the effective SXT temperature will obviously be larger than the temperature at the very "base of the corona", since the model temperatures increase monotonically with height initially. But how much larger is this systematic error in the measurement?

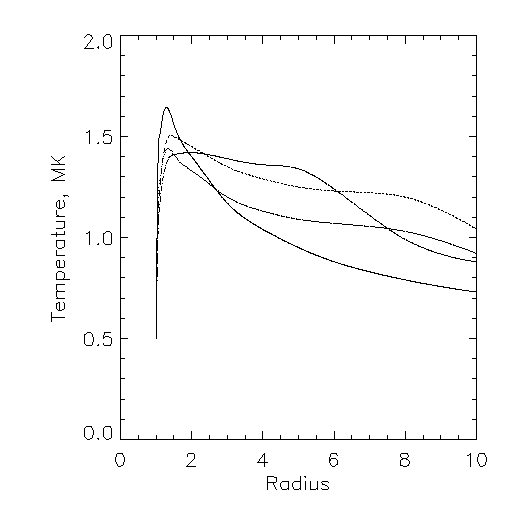
    In the plots above, the Y-axis has known but somewhat irrelevant units. But of course the values for 1.5 radii are small - the X-ray corona rapidly becomes dim for larger impact parameters. The bias in temperature varies with height for these models.

    The vertical case is unique: by using the DEM in the plot on the upper left, we find a maximum effective temperature of TT1, for Withbroe model N1 ("quiet corona"), and a minimum temperature of TT2 for model N2 ("polar hole, minimum"), which seems plausible. Both of course greatly exceed the temperature of the base of the corona in the models, since hotter material at higher altitudes contributes to the integration.

    As a function of impact parameter, we get the following plots of the temperature error resulting from the DEM consideration:

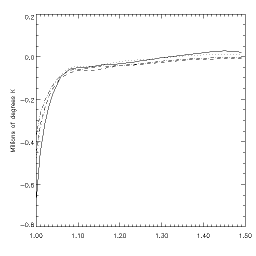
    where the different line styles show the four different Withbroe models. We see a systematic discrepancy, but it's less than 0.1 MK above 1.05 solar radii for all cases. Near the Sun, the apparent temperature is always higher than the true plane-of-the-sky temperature because the line of sight samples higher altitudes, and the temperature increases with height in this region of the models. It's hard to say how seriously to take this - the Withbroe models, now senior citizens in the coronal-modeling effort, probably have large errors at low altitudes anyway. On the other hand there are no recent comprehensive models that I'm aware of - let me know if they exist, and I'll re-do this analysis.

    So what?

    We don't find extremely large temperature discrepancies, but they are significant (or should be so) to coronal modelers. The line-of-sight integration over models of this type results in an observational bias. It's an illustration of how one characterizes such a bias, which many astronomical observations unfortunately must deal with, by using a "forward-method deconvolution". The alternative to this, a mathematical inversion of the data to produce two model-independent functions (density and temperature) is beyond the talents of the author, but there are people out there who probably can do it.

    I know that these plots are tedious by comparison with our beautiful pictures, but... we need to be quantitative!


    April 2, 2000 H. S. Hudson (hudson@lmsal.com)