Michael's Log II
Wednesday 6th of July
So The past few days I have made a reasonable degree of progress with finding a general distribution for null points. It has become clear that the previous method is far too cumbersome, involving a lot of integration with summations. Instead, the function previously written, g_eval, was used to evaluate g for every point height by inputting the corresponding C value. First, here is how each variable calculated from the spectral integrals varies with height.
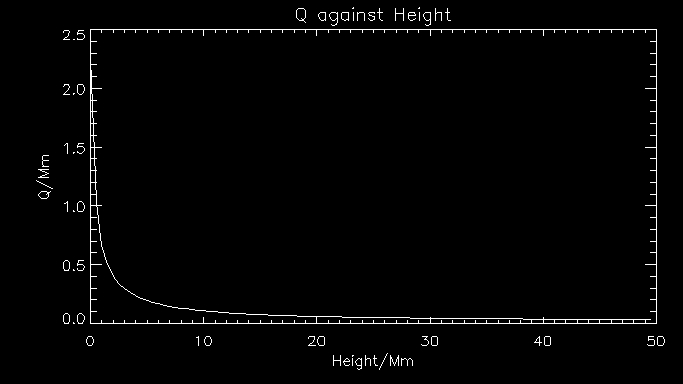
This is a graph of q against height in Mm
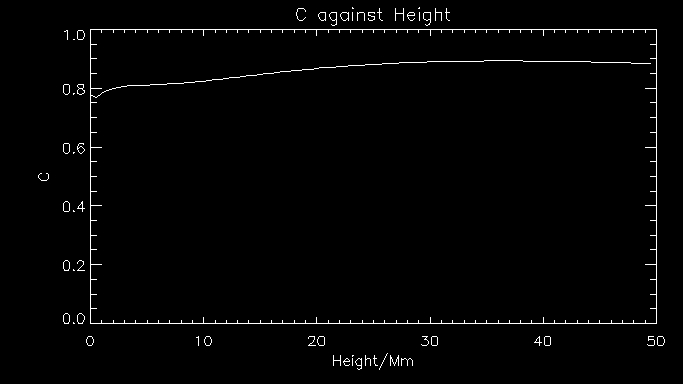
This is a graph of c against height
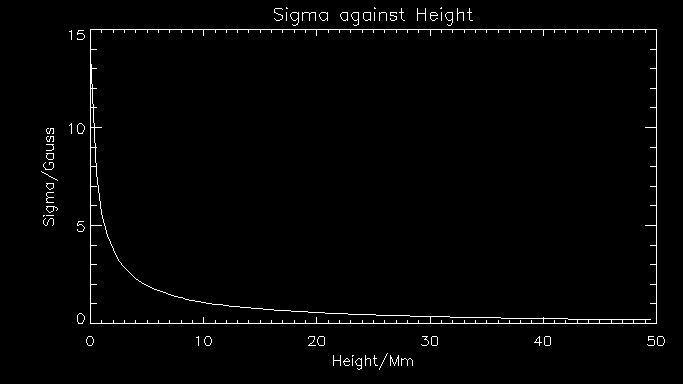
This is a graph of sigma against height

This is a graph of g against height
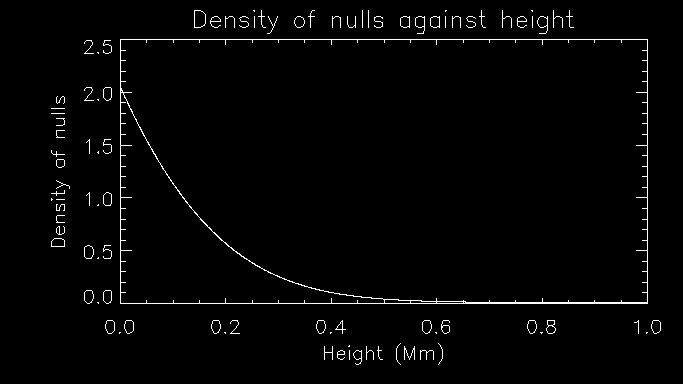
This graph represents the density of nulls at different heights. As you can see there is a massive tailoff, which you would expect, with height.
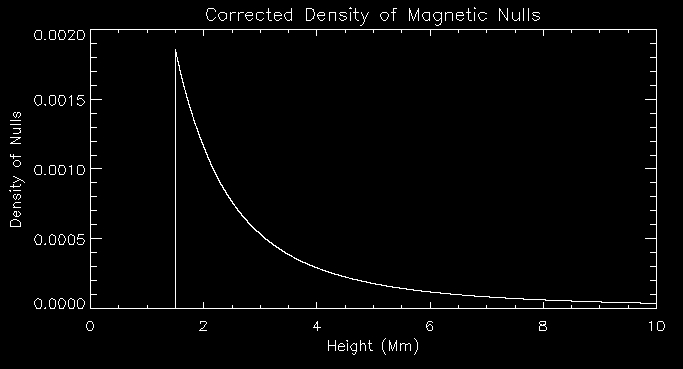
Finally, this is a graph of null point density vs height above 1.5Mm and with it's power spectral density corrected for noise.
Integrating this graph over all heights will give us the number of nulls per square Mm found in a column above the photosphere. Dana Longcope and Clare Parnell found a value of 0.0031 on average. As you can see by this next graph, I got a similar result.
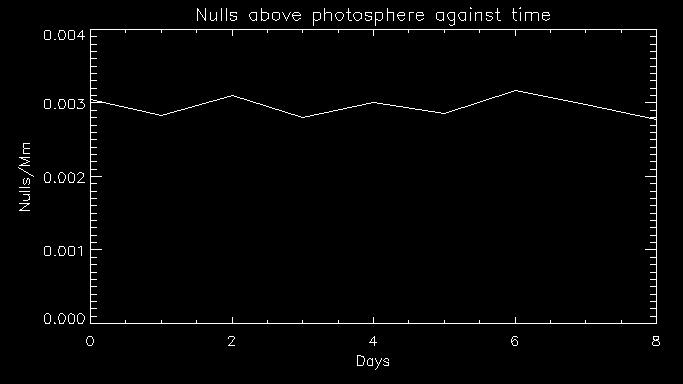
This is the total nulls above the photosphere per Mm squared on for just over a week
In total this is typically close to 20000 null points above the solar surface, one just under every 300 Mm squared.
Now we are going to look more at the determinant of the jacobian matrix of the magnetic field
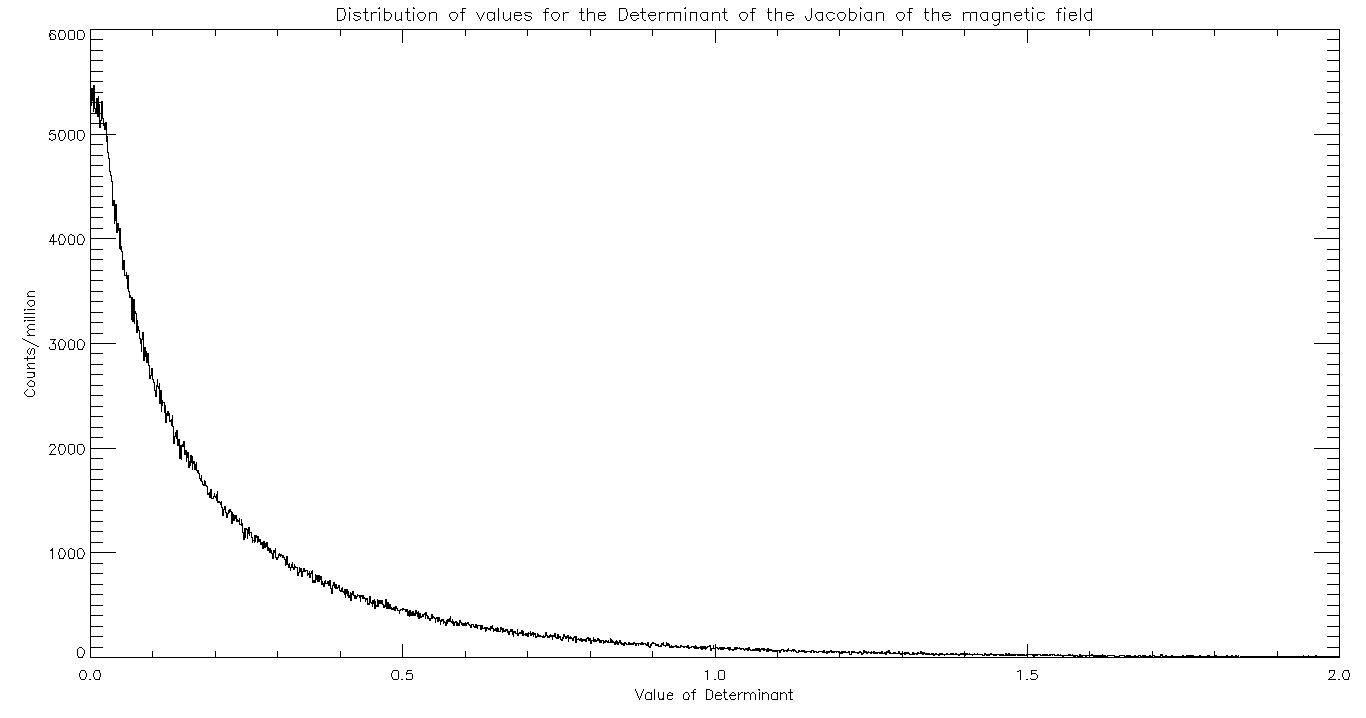
This histogram of the value of the determinant of the jacobian illustrates that most of the values are quite small, and the smallest ones are the last to be discarded. So as long as the cutoff is on the order of 100 then almost every value should be retained and the Density of nulls will resemble the uncorrected one.g
So it turns out i've been thinking about this from the wrong perspective. should actually be
should actually be  . To see why, we should examine the mathematics of the situation a little more. Here is the equation for Alfven frequency
. To see why, we should examine the mathematics of the situation a little more. Here is the equation for Alfven frequency  This corresponds to an Alfven wave we are generating, with a given frequency. From this frequency, we can determine what the value of determinant the jacobian of the magnetic field has to correspond to in order for the wave not to get reflected. If this value of Wcutoff is higher than the actual determinant then at the same height then we keep the value. If not we discard it.
This corresponds to an Alfven wave we are generating, with a given frequency. From this frequency, we can determine what the value of determinant the jacobian of the magnetic field has to correspond to in order for the wave not to get reflected. If this value of Wcutoff is higher than the actual determinant then at the same height then we keep the value. If not we discard it.
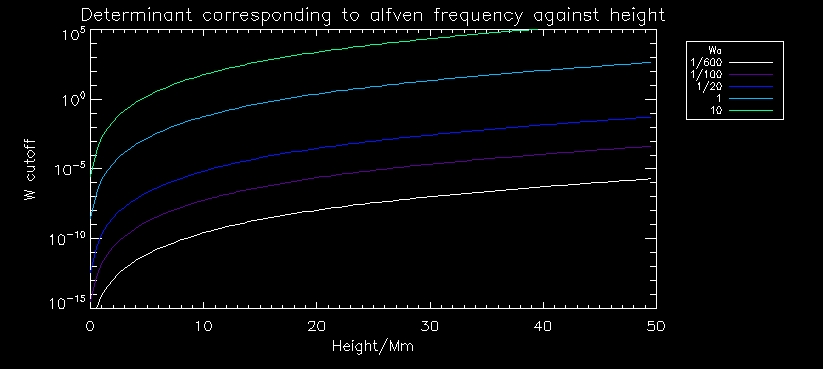
This cutoff determinant is given by

So we essentially need to satisfy the relation

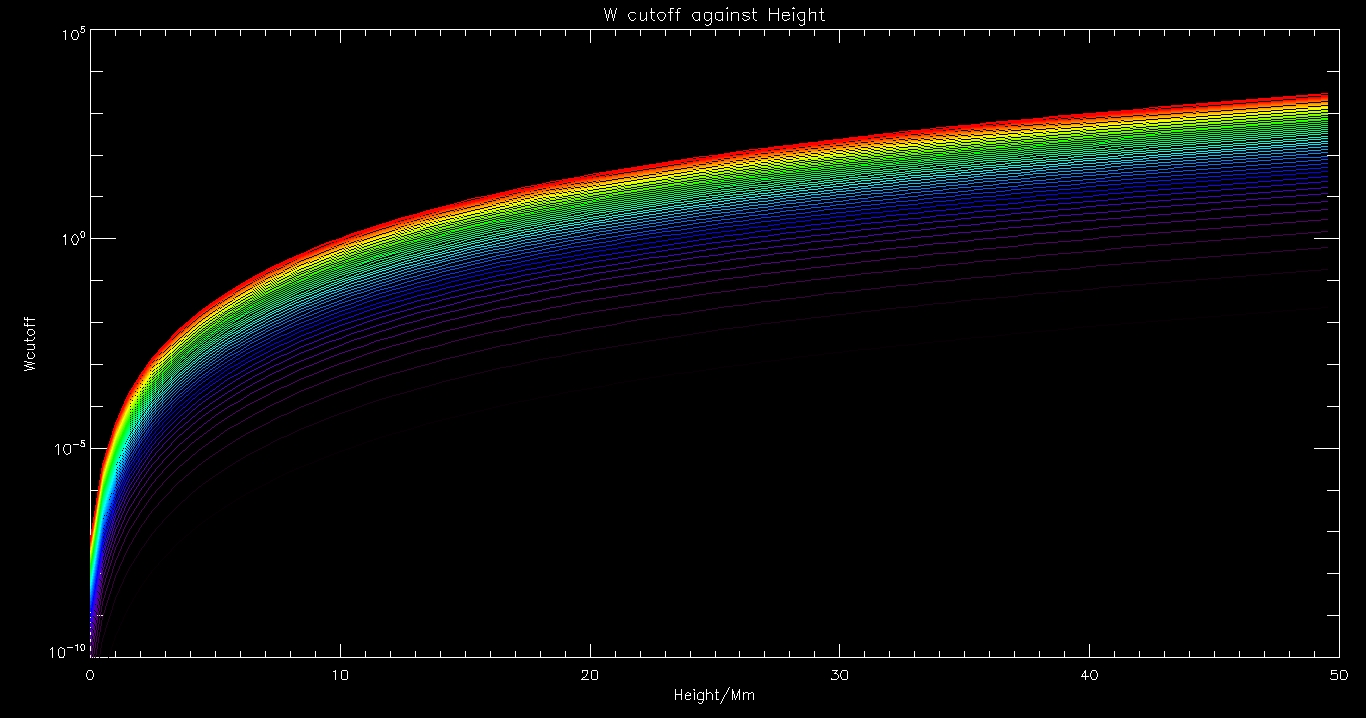
So with this in mind, lets see how this corresponding determinant varies with height, for different frequencies of alfven wave.
Now let's look at what the dimensionless function G looks like at for wave frequency of 2 (Not actually sure what the units are yet, shall figure that out later.
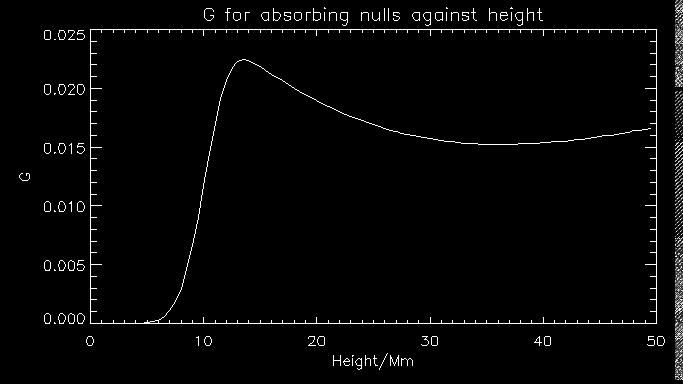
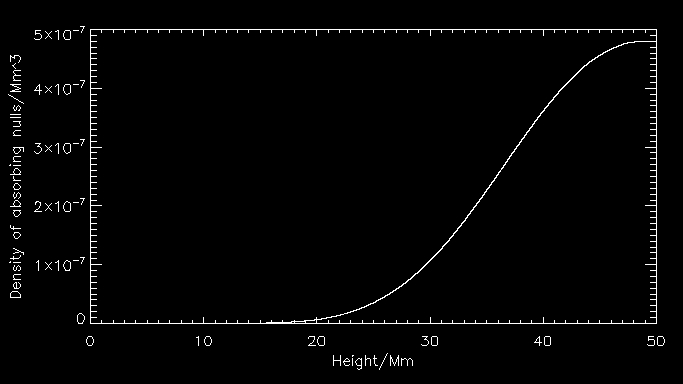
Finally, here's is the density of nulls for these conditions.
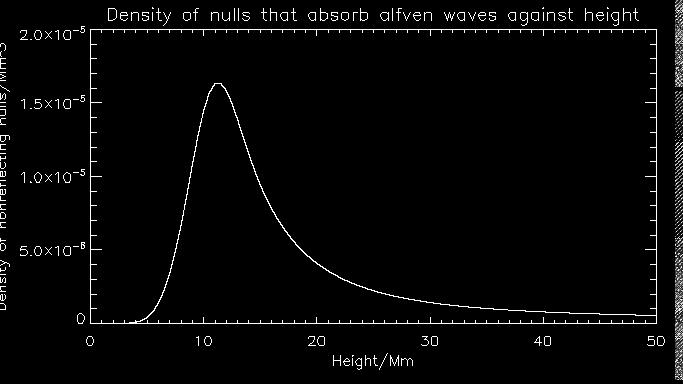
As you can see, instead of the majority of nulls peaking at very low heights, it is actually peaked somewhere around 12 Mm. This is because the Wcutoff is very low at small heights, and only a minute fraction of the determinants of the jacobian of the magnetic field are below this, while at greater heights Wcutoff is much higher. What fraction of the total nulls comprise of these special nulls? Just over 5%, so there are about 900 of these nulls in above the photosphere.
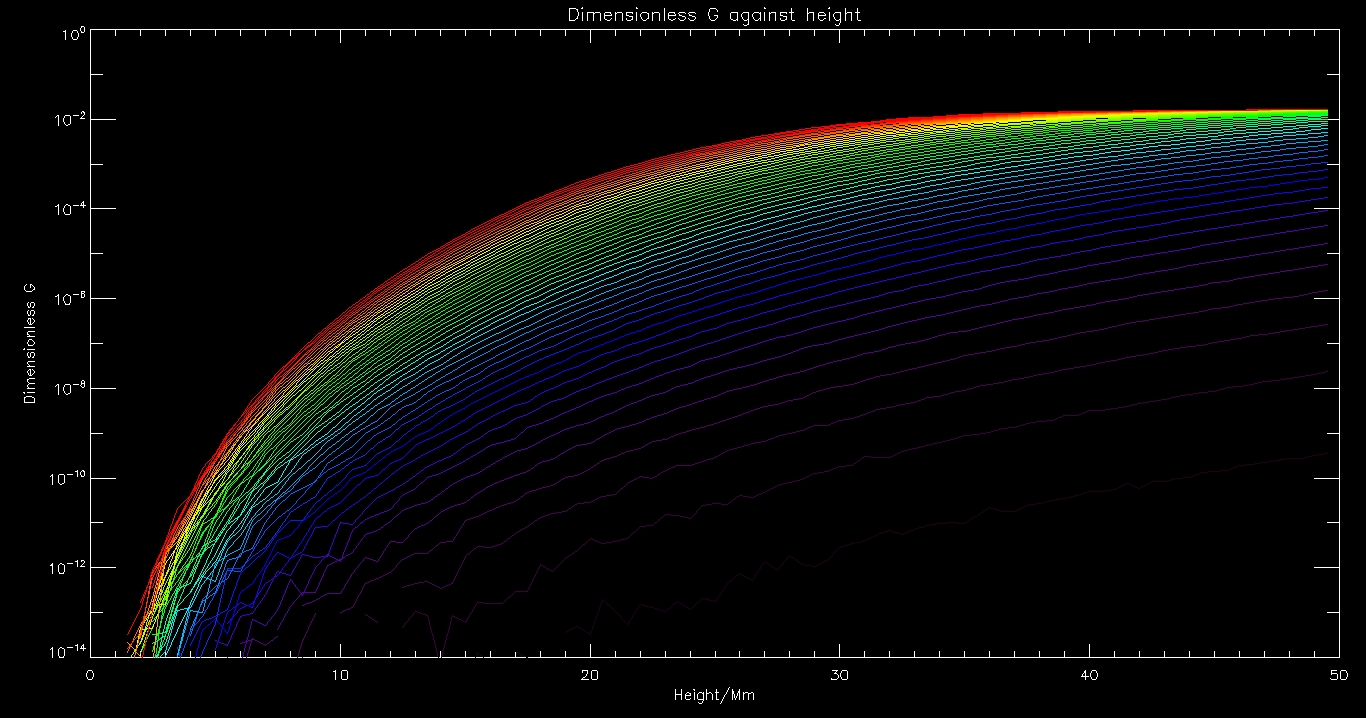
Now for some even cooler graphs. Here is one where we have chosen frequencies in increments of 0.01 Hz (purple) to 0.5Hz (red)
Here is a similar graph, this time for G(z) 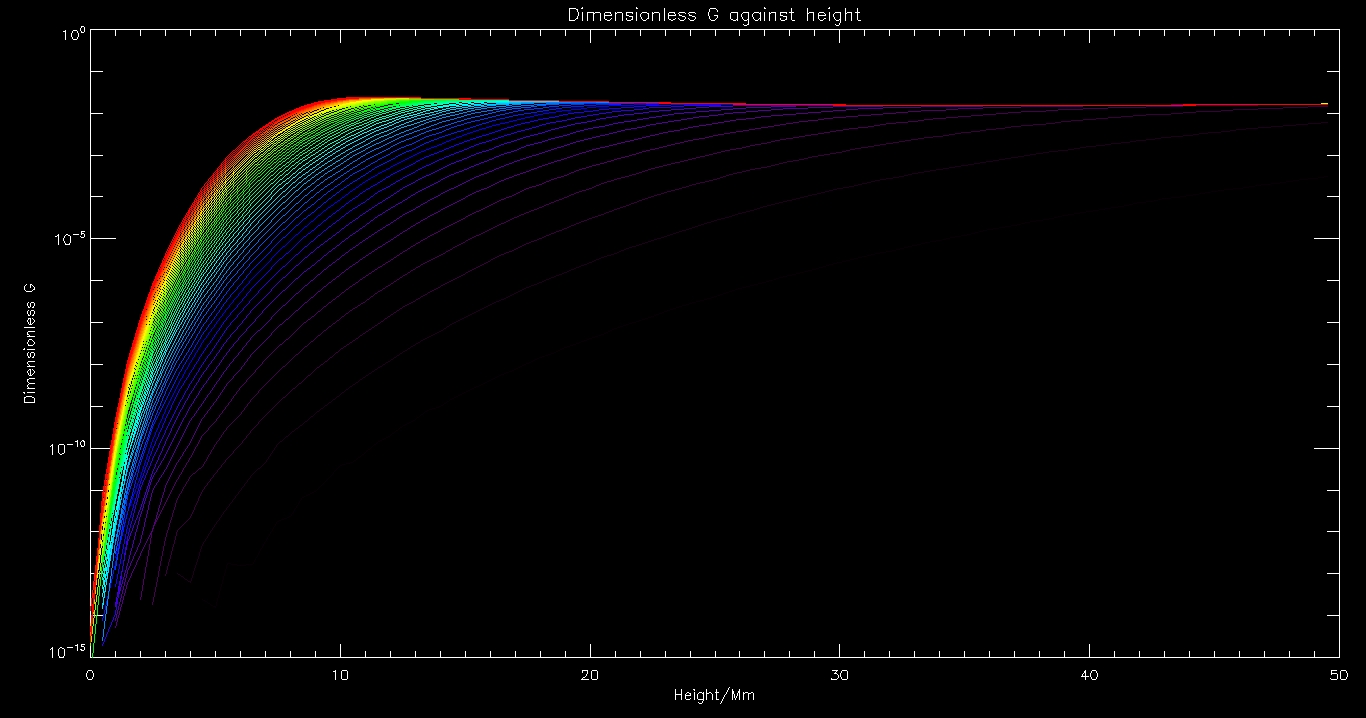
Here is the equivalent for the density of nulls 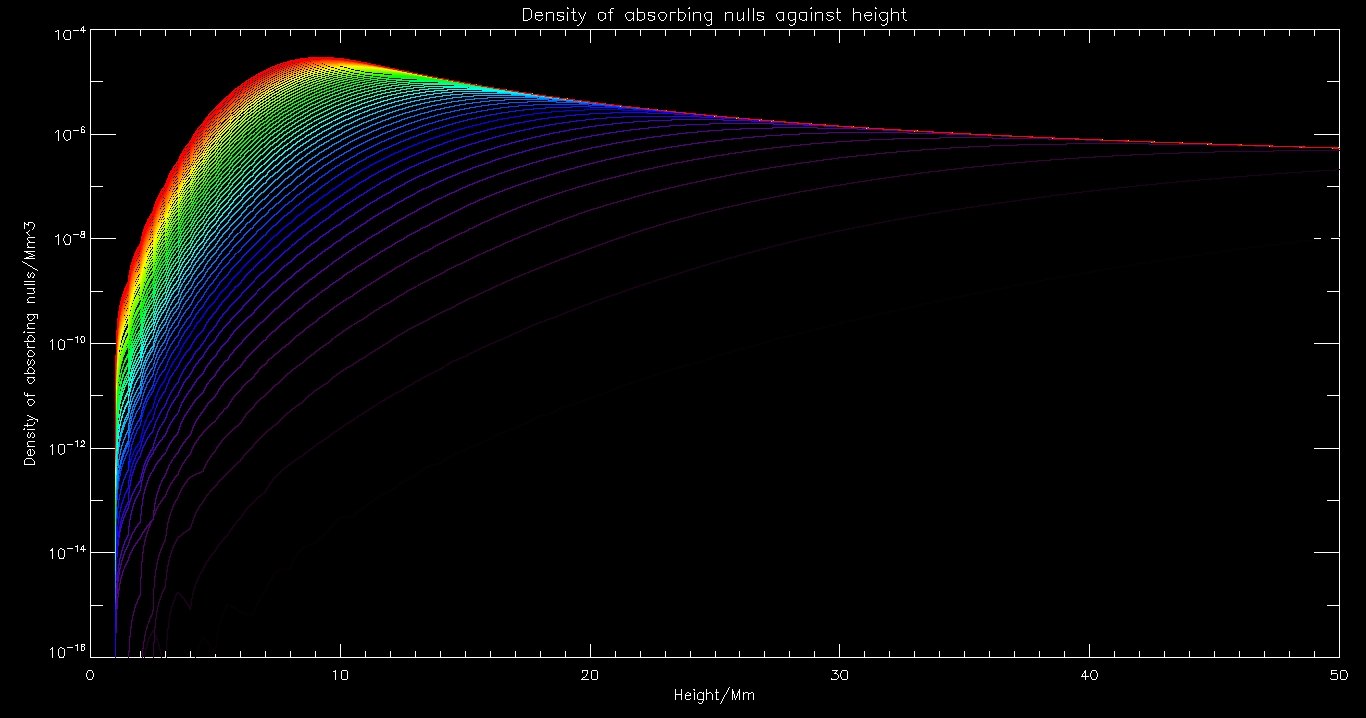
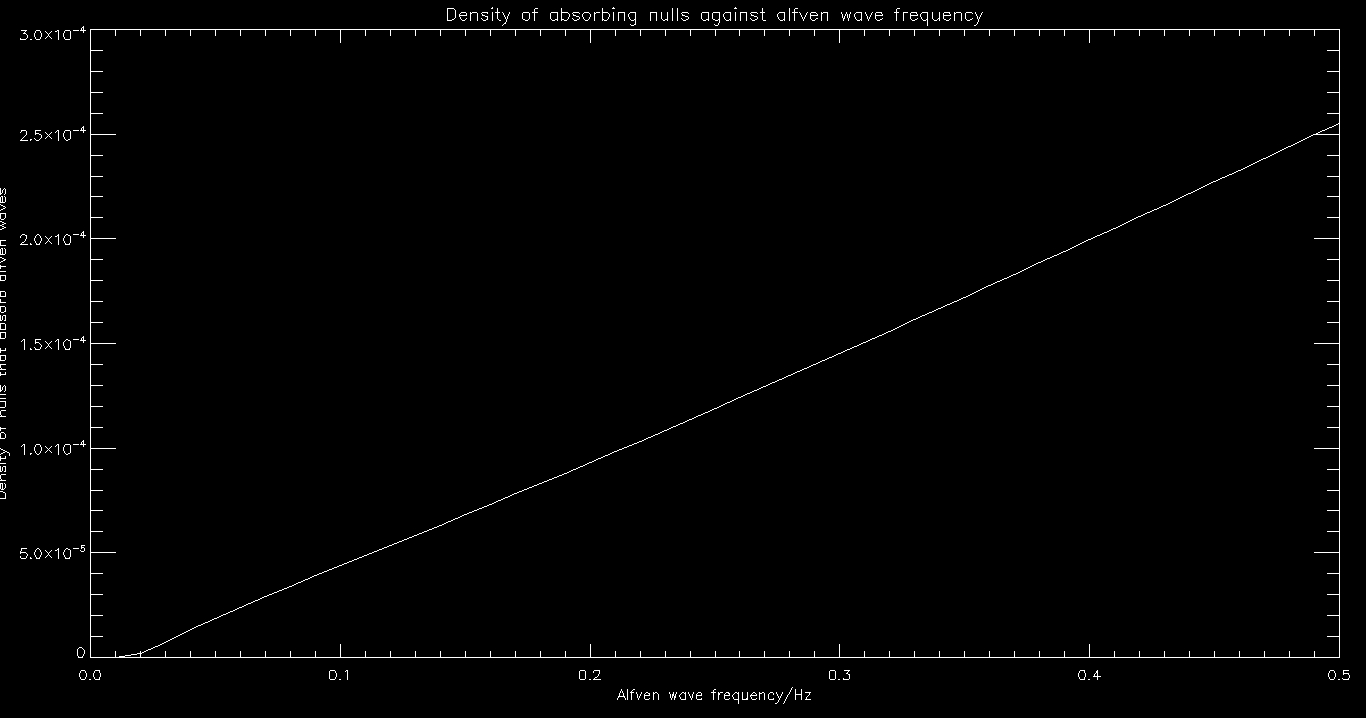
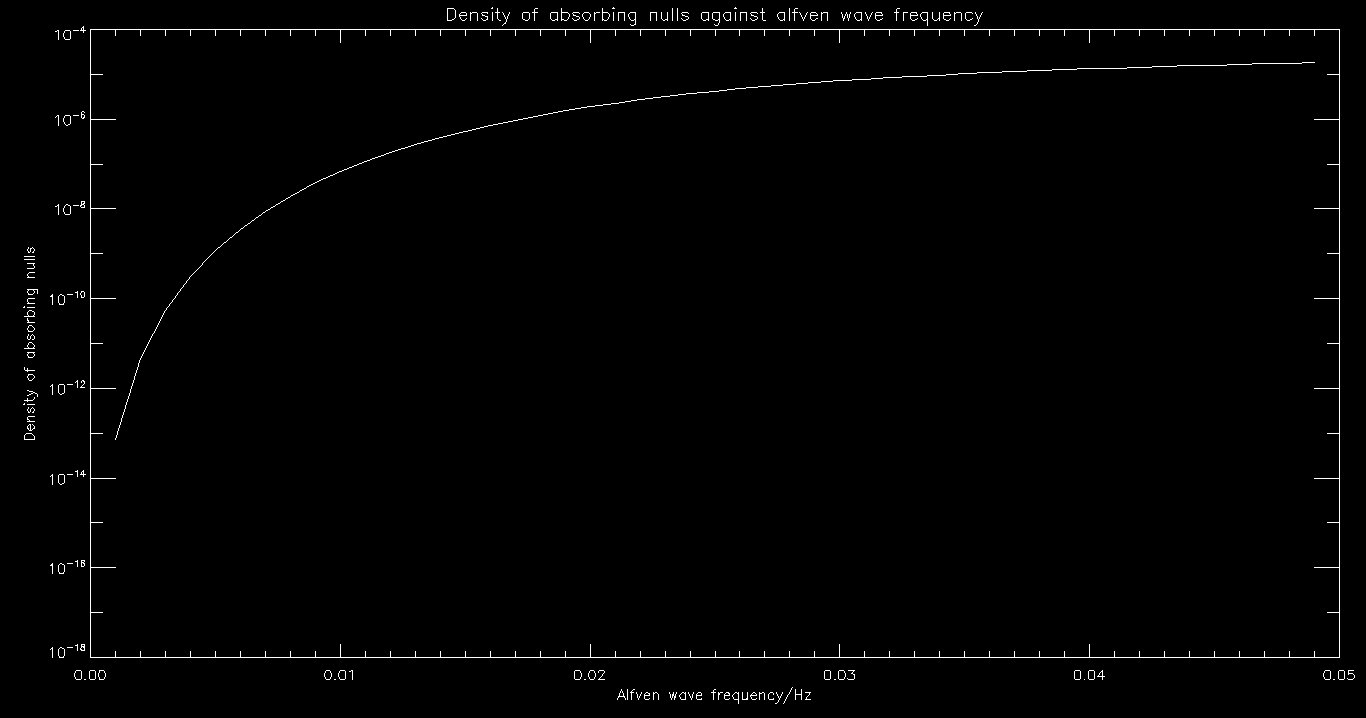
Here is a graph of frequency vs the number of nulls that absorb that specific frequency.
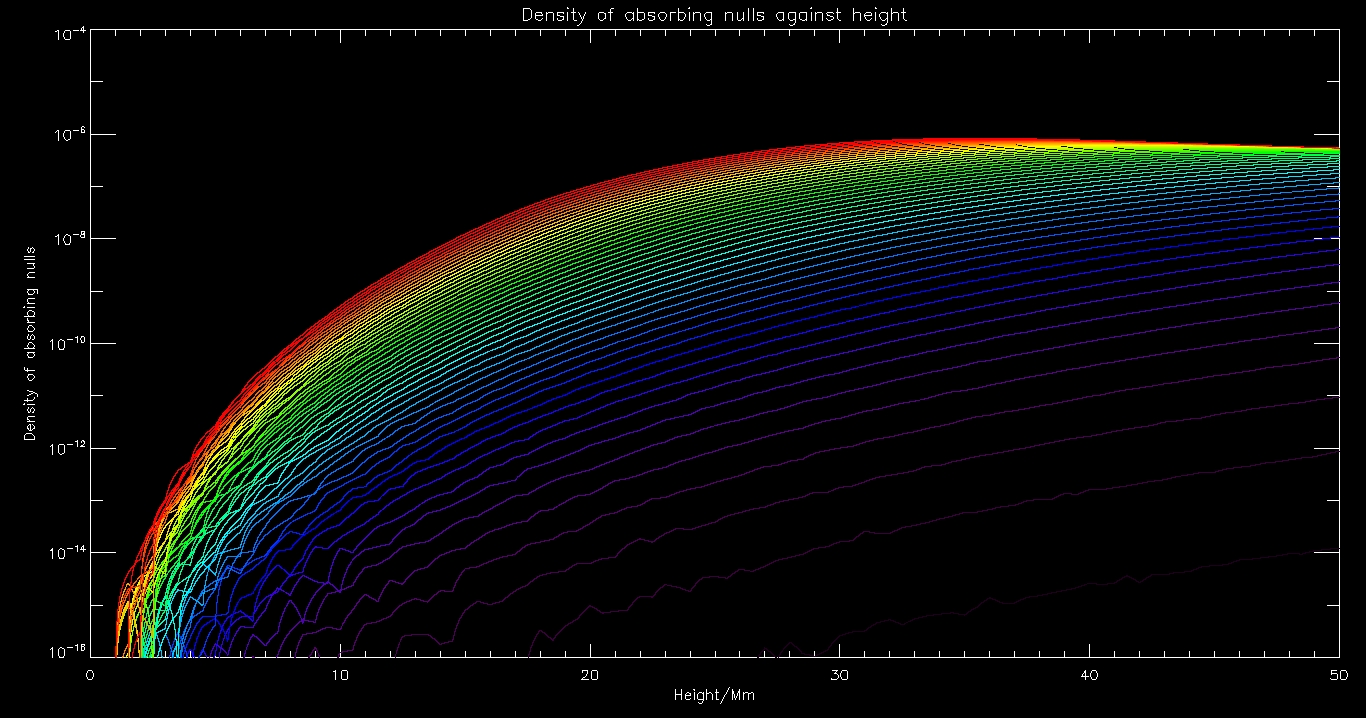
I repeated the same anaylsis for waves with a much higher period. This time the range is 0.001 to 0.05 in increments of 0.001

It seems we are coming to the end of this project. One thing that needs to be looked at however are the energy spectrum of waves emitted by the suns' photosphere and what heights this might correspond to. So from Milano, Gomez and Martens 1997 we find that the frequency dependence of the kinetic energy spectrum of the photosphere is proportional to a negative power between 1 and 2.5. Explaining this a bit - there are two main peaks in the suns photospheric kinetic energy spectrum. There are waves generated due to granulation, which tend to last 8 to 20 minutes, producing very low frequency waves. The second peak is due to acoustic waves which are very strongly peaked at 2-4 mHz, which is way too low to have any appreciable effect (at that frequency is it unlikely that there is even one null point in the corona that would be able to absorb it) after that there is a rapid decay in the energy spectrum.
So what does this spectrum look like when multiplied by the density of nulls for a specific frequency? Well since it is very difficult to determine any prefactors we shall have an entirely arbitrary y axis, so it has been normalised.

So now we have a few specific peak frequencies to deal with, for different values of beta. So depending on what beta is, we expect the most heating at different heights. A value of beta = 1 seems very unlikely though in all actuality, it does not seem physical for motion on the photosphere to produce enough very high frequency waves to give an energy spectrum favouring higher frequencies. Taking beta = 2.5 we find that the peak heating should occur at roughly 50 Mm
 This would correspond to roughly 100 nulls in the solar corona absorbing the most energetic frequency, but not that much heating would be provided from other frequencies due to the sharp peak in the energy spectrum. If beta was 1.5 however, there would be 150 nulls doing the most heating but 1500 nulls contributing to heating at least half as much. This holds out some hope for the theory that alfvenic wave heating can make a difference to the solar corona.
This would correspond to roughly 100 nulls in the solar corona absorbing the most energetic frequency, but not that much heating would be provided from other frequencies due to the sharp peak in the energy spectrum. If beta was 1.5 however, there would be 150 nulls doing the most heating but 1500 nulls contributing to heating at least half as much. This holds out some hope for the theory that alfvenic wave heating can make a difference to the solar corona.








 should actually be
should actually be  . To see why, we should examine the mathematics of the situation a little more. Here is the equation for Alfven frequency
. To see why, we should examine the mathematics of the situation a little more. Here is the equation for Alfven frequency  This corresponds to an Alfven wave we are generating, with a given frequency. From this frequency, we can determine what the value of determinant the jacobian of the magnetic field has to correspond to in order for the wave not to get reflected. If this value of Wcutoff is higher than the actual determinant then at the same height then we keep the value. If not we discard it.
This corresponds to an Alfven wave we are generating, with a given frequency. From this frequency, we can determine what the value of determinant the jacobian of the magnetic field has to correspond to in order for the wave not to get reflected. If this value of Wcutoff is higher than the actual determinant then at the same height then we keep the value. If not we discard it.












