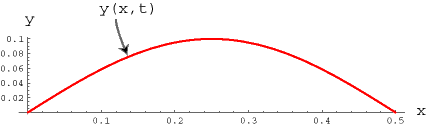
[8]
A one dimensional wave equation can describe a vibrating string with tension T
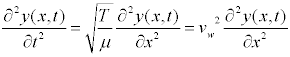
where v is the wave velocity along the string
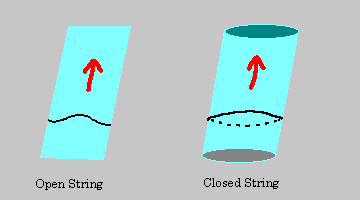
given certain, different bounary conditions this mehtod
can explore open strings and closed strings
For open strings there are two main boundary conditions
for Neumann boundary conditions the endpoint is free to move about but no momentum flows out
if the Dirichlet boundary conditions are considered -where the ends of the strings are held at specific locations on a manifold
the classical solution can be
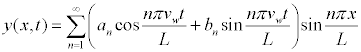
this is the non-relativistic solution
for the relativstic case a similar solution is produced
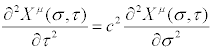
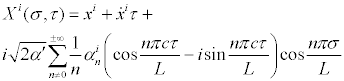
with string mode action from Euler-Lagrange equations for a world sheet
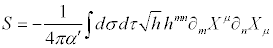
[8]
The string tension in string theory is denoted by the quantity 1/(2 p a'), this is equal to the square of the string length scale.
This sets the length of the string at around the Planck lenth 10^-33 cm
These strings span out a 2-d space in time called world sheets ,(this is similar to 0-d particles -world line)
[9]
For open strings there are two main boundary conditions
for Neumann boundary conditions the endpoint is free to move about but no momentum flows out
if the Dirichlet boundary conditions are considered -where the ends of the strings are held at specific locations on a manifold
the classical solution can be
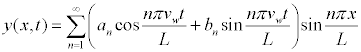
this is the non-relativistic solution
for the relativstic case a similar solution is produced
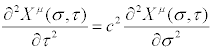
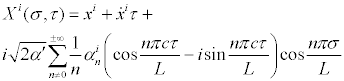
with string mode action from Euler-Lagrange equations for a world sheet
[8]
Fixed string tensions represent the elementatry particles
vibrating with thier own specific frequencies
The string tension in string theory is denoted by the quantity 1/(2 p a'), this is equal to the square of the string length scale.
This sets the length of the string at around the Planck lenth 10^-33 cm
These strings span out a 2-d space in time called world sheets ,(this is similar to 0-d particles -world line)

[9]