|
ROLE Leader: |
NAME - print ____________________ ____________________ ____________________ ____________________ |
-sign ____________________ ____________________ ____________________ ____________________ |
Learning Objectives
1. Become familiar with the celestial sphere, zenith, and celestial pole.
1. Become familiar with the stars' paths across the celestial sphere.
Text reference: Section 1.1, pp. 18-22.
Whoever is today's leader should read each section aloud as you come to it.
For the rest of the course, you'll have already read about each activity's subject before we do
the activity. But that's impossible today, so I've summarized the text's Section 1.1 below.
Since I can't write as well as the text's authors, my explanation isn't as good as theirs -- my
apologies! Further, I have only guessed about how long this exercise will take -- if it's taking
too long, we'll cut it short.
I. Introduce yourselves and shake hands, please!
II. The celestial sphere is an imaginary spherical surface which surrounds the Earth, on which the stars are located. Its axis lies along the Earth's, a line through the terrestrial north and south poles. The Earth blocks half of this celestial sphere from view at any instant, but, because of the Earth's rotation, many stars on the sphere rise in the east and set in the west -- just as you know the Sun does.
Points on the celestial sphere correspond to points on the Earth: examples include the north celestial pole, which lies directly over the north terrestrial pole, and the celestial equator, which lies over the terrestrial one. Whatever point on the sphere that lies directly over your head is your zenith. As the earth rotates, your zenith point moves along the celestial sphere. Thus, different celestial points -- those at your latitude -- become the zenith point for an instant.
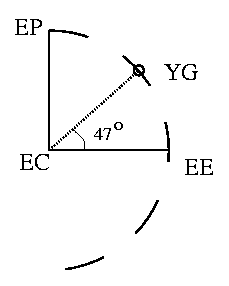
Suppose your group is standing at latitude 47o N. We're going to find the angular altitude of the north celestial pole above your northern horizon. Let's work though this brief review of high school geometry in steps. In the cross section of the Earth drawn below, your group is labelled YG, and the Earth's equator, center, and north pole are labelled EE, EC, and EP, respectively. Work in pencil, please.

1. Extend the line from EC-YG beyond YG, and label it line #1.
What celestial point does this line run toward? Label the celestial end Z for this point.
2. Now draw a line through YG that is perpendicular to the line you just drew,
labelling it line #2. This line's ends point to your group's celestial horizon --
the boundary between stars you can see and those you cannot.
Label it's upper end NH, for the northern horizon.
We want to find the angular height of the celestial pole with respect to this line.
As an aside, what is the altitude of your zenith with respect to this line?
3. Now draw a line parallel to the line EC-EP through YG, and label it line #3.
Label the point where this line intersects the line EC-EE point HR
(for hot rock, which is all there is at HR).
This line points to the north celestial pole; label its top end CP.
Just to confuse you, the line EC-EP also points to the celestial pole. How far away must the
north celestial pole be for these lines to really be parallel?
4. You know the angle YG-EC-HR is 47o. If you've drawn line #3 correctly,
then angle EC-HR-YG is 90o. What is angle HR-YG-EC? (Recall that triangles'
interior angles add to 180o.)
5. Recall that ``vertical'' angles are equal.
How does angle Z-YG-CP compare to angle HR-YG-EC?
6. Since you drew line #2 perpendicular to line #1, you can now find NH-YG-CP, the angle between
the northern horizon and the celestial pole that your group sees. What is it?
7. True or false: The altitude of an oberserver's celestial pole equals that person's
latitude.
III. Now imagine that the Earth is standing still, and the celestial sphere is rotating overhead. Suppose your group stands at the Earth's equator. Picture the path a star exaclty on the celestial equator takes as it rotates past, first rising in the East and setting in the West.
1. What is the shape of its path across your sky?
2. What is the path of a star near the celestial equator across your sky?
3. Do all the stars you see from here take similar paths?
4. Do any stars you see not rise and set?
IV. Now suppose your group stands at the North Pole. Polaris, a.k.a., the North Star, is quite near the north celestial pole, which is now your zenith.
1. Pretend Polaris is exactly at the celestial pole. Does it move, rise, or set?
2. What path do stars near Polaris take? Do they rise or set?
Would the term circumpolar be appropriate for these stars?
3. A Hard Question: If you're not at the pole,
what is the angular width of the circumpolar region?
V. Study the star chart, a ``map'' of the night sky at an intermediate latitude, roughly
that of Montana. On terrestrial maps, east is to the right and west is to the left,
but the opposite is true for this celestial map. Why?
Now suppose your group goes stargazing, and you follow the paths of some stars in the chart.
On the chart, use a pencil to draw the paths of the following celestial objects:
A) any star in Ursa Minor (a.k.a., the Little Dipper) other than Polaris;
B) the southern-most star in Scorpius; C) the asterism, or star grouping, Delphinus.
(Hint: Since your latitude is intermediate between the terrestrial pole and equator, you might expect
some stellar paths to be similar to those seen from the equator, and some to be similar to those
seen from the pole.)
VI. Please discuss the following questions and agree upon an answer.
How many minutes did this activity take your group?
Was this activity too easy/about right/too difficult for your group?
Were there too few/about right/too many concepts?
Were the explanations too long/about right/too short?
What section(s) did you most like?
VII. The Greeks mistakenly thought the celestial sphere rotated about the Earth.
Try to think of ways to show that the Earth is rotating, not the celestial sphere;
spend the rest of the class time discussing ideas. Draw pictures on the scratch paper to
help explain complex ideas. Do not worry if you cannot -- this is not an easy thing to show!
List any ideas here, with a brief (1 - 2 sentence) description of your "rotation detection" ideas.