Zoe Sturrock: Research log for Summer 2012 Solar Physics REU at Montana State University, Bozeman, MT Home Project Summary Inferring Magnetic Reconnection from UV Signatures in Flares Solar flares are spectacular energy release events in the Sun's atmosphere. It is understood that the energy to fuel flares is provided by the Sun's magnetic fields, most probably through a physical process called magnetic reconnection. Magnetic reconnection changes the way magnetic field lines connect to the Sun's surface, and the subsequent energy release is often manifested as heating along a magnitude of newly formed magnetic flux tubes. In my project, I will study the evolution of flare radiation signatures at the foot-points of magnetic loops formed during reconnection, measure important parameters of magnetic reconnection, and search for better understanding of the relationship between magnetic reconnection and energization of plasmas or particles in flux tubes. I will analyse and model imaging observations of solar flares and magnetic fields by the satellites TRACE, SoHO, RHESSI and SDO. Dates:06-07 June For my first introductory IDL assignment I was given a set of UV images obtained by AIA/SDO in two wavebands: UV 1600 and UV 1700, and was given the task to analyse them. I first decided to compare the 1600 images and 1700 images at a given moment in time. We can then compare a given image at two different wavelengths. 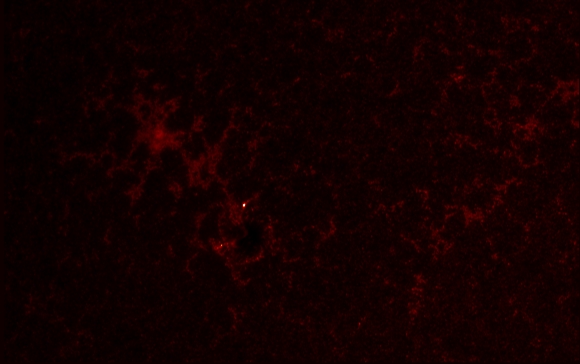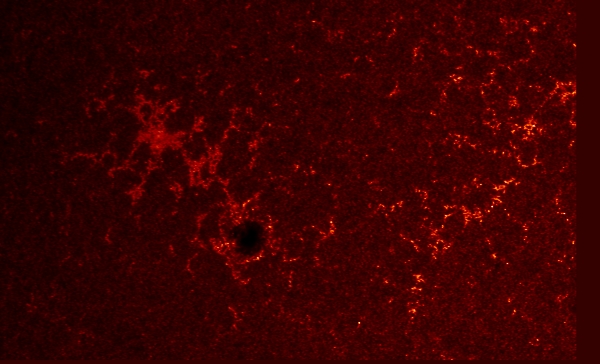The UV 1600 image is given as follows: At the same moment in time the UV 1700 image is: I was given a file that contained the 804 brightest pixels in the 1600 images. 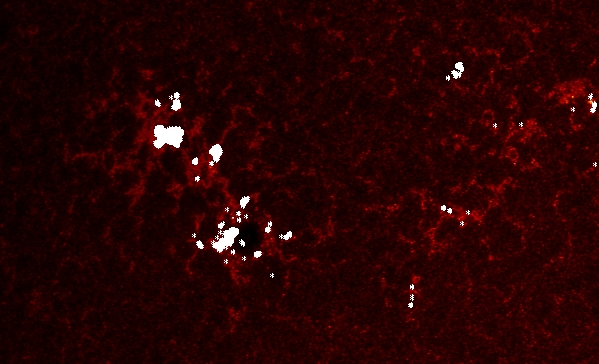I displayed the location of these pixels by superimposing symbols onto a 1600 image: To do this I used the following commands: tvscl,DAT1600(*,*,8) for i=0,803 do xyouts,xx(i),yy(i),'*',/dev,align=0.5 I then looked at the time history (often referred to as a 'light curve') of the brightest pixel of the 1600 image. This curve is the result of plotting time against intensity. 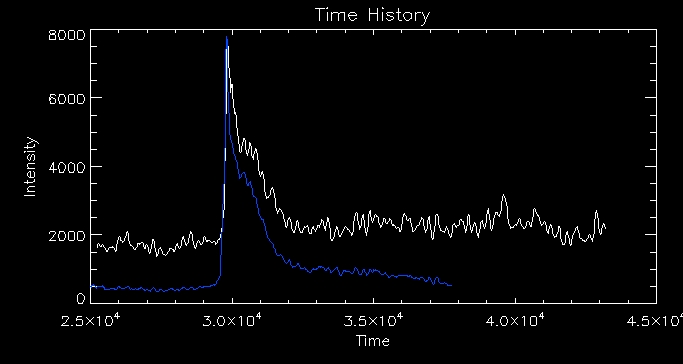The white line represents the intensity of the pixel in the 1700 image and the blue line represents the 1600 image. Dates:08 June Today I looked through 'Highly Efficient Modelling of Dynamic Coronal Loops'; a paper by Klimchul et al. and Cargill et al. This paper looks at the EBTEL model ("enthalpy-based thermal evolution of loops" which accurately describes the evolution of the average temperature, pressure and density along a coronal strand. This model is a highly efficient "0D" model (named this as it only has one average value of temperature, pressure and density at any given time in the simulation) which improves significantly upon previous models of this type. Loops are modelled as individual flux tubes or 'strands'. To understand the EBTEL model, we must first understand the process which leads to solar flares. Magnetic reconnection is a process which forms flare loops and whereby free magnetic energy is released which heats the chromosphere forming flare ribbons. Magnetic reconnection is observable so we can measure the magnetic reconnection rate. As I said previously this leads to energy release. We can fit a heating function to this by studying the observed UV light curve e.g. gaussian, triangle etc. This causes the plasma to evolve and this is what we simulate using the EBTEL model. Lastly, this leads to flare radiation which we can observe and feed back into our model. The basic principle of EBTEL is to equate enthalpy flux of evaporating or condensing plasma with any excess or defecit in the heat flux relative to the transition region loss rate. 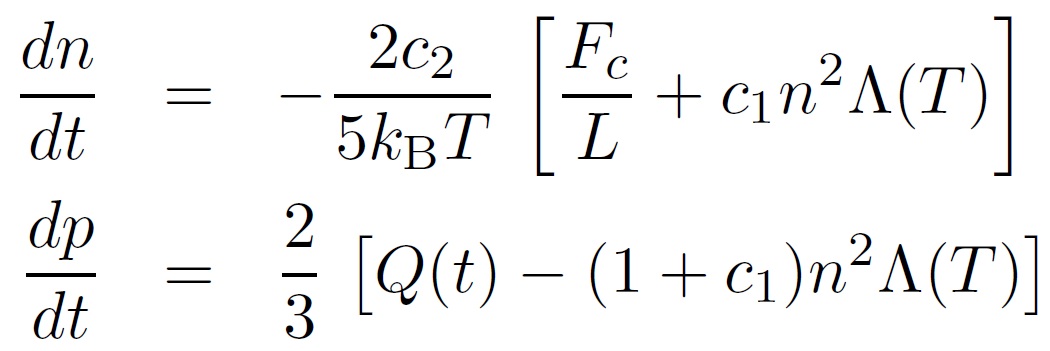The EBTEL model consists of two equations governing the evolution of electron number density and pressure: The first equation is a mass conservation equation, and the second a thermal energy equation. Q(t) represents the heat input and is governed by our heating function. Fc is the conduction flux, Λ(T) the radioactive loss function and L the half loop length. the only free parameters are c1 which is a constant characterising the ratio of the total energy loss through the transition region to the radiation loss through corona and λ (where Q(t)= λI). c1 has been assumed constant in the past, but the best matched constant has been shown to be different for different loops, so evidence suggests that it should be a variable. In my project I will look into the possible forms of this parameter. The main advantages of the EBTEL model are that it provides the DEM(T) of the transition region and can account for non-thermal electron beams and heat flux saturation. Dates: 12th-13th June For the past few days I've been looking at the IDL procedure which runs the EBTEL model.  Initially I used the default parameters in the code and started to look at the output of temperature, density etc. of the coronal strands. I first looked at the temperature profile of the brightest pixel and observed that there is a sharp rise in temperature at 140 minutes after 6UT then the temperature slowly decays. 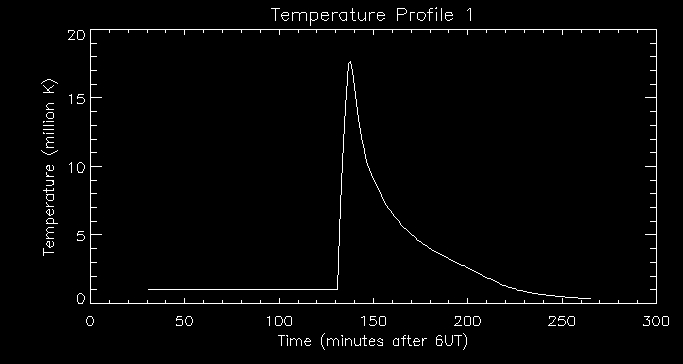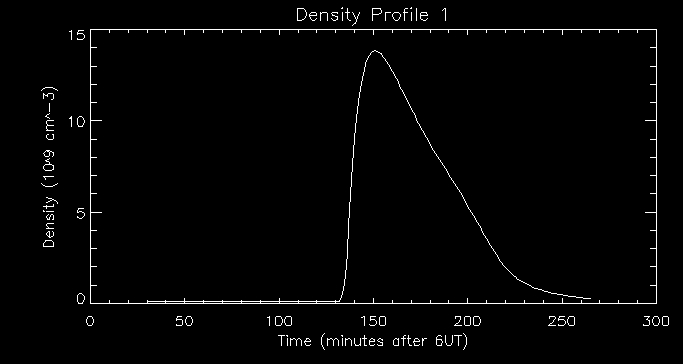I then looked at the associated density profile: We can see that there is a time lag between the peak in temperature and the peak in density. The rise in temperature in the coronal loop causes thermal conducion which transfers energy to the transition region. This heats up the transition region. The transition region must then lose energy by radiation and other means (i.e. conducting energy further down). When there is an imbalance between conduction from above and loss of energy (radiation and conduction further down) there is an upflow which carries mass into the corona. This causes the coronal loop to become more dense as evidenced by the graph above. The peak in density is at about 155 minutes after 6UT. We can also look at the associated light curve for this particular pixel. 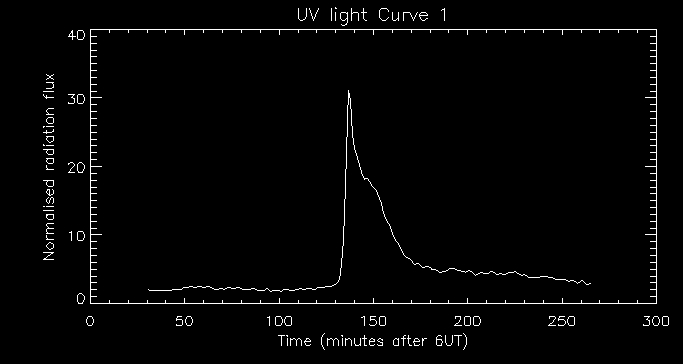We can see a rapid rise in the radiation flux at about 140 minutes after 6UT which only lasts a few minutes and a gradual decay lasting tens of minutes.  This agrees with the temperature and density profiles produced.  This indicates an impulsive energy deposit in the lower atmosphere and subsequent coronal evolution. Next I will look into how varying model input parameters affects the output of temperature and density. I will adjust three parameters; c0 (defined as λ previously) which scales UV counts to energy, c1 which scales loss through the base of the coronal loop and c4 which is the ratio of beam-driven upward flux to heating flux. Date: 14th - 15th June Today I began to play with the parameter values c0, c1 and c4. There is a built in procedure run_ebtel_new which performs a few parameter runs taking three values of c0 and c1 ([1,2,3]), and three values of  c4([0,0.4,0.7]) and loops round them. We therefore performed 21 different parameter runs. I will select a few to display here, to show how varying the parameters affects the dynamics of the system.  The graphs above are for the case c0 =1, c1 = 1 and c4 = 0. 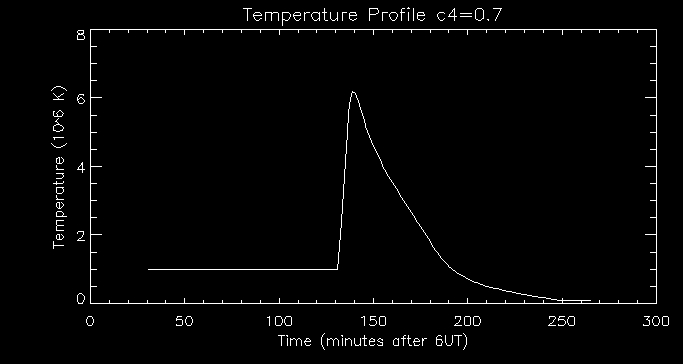Let's look at how increasing c4 affects the temperature and density by taking the case where c4 = 0.7: We can see that the temperature peaks at around 6M K, which is much lower than previously. Increasing c4 increases the ratio of beam-driven upward flux to total heating flux which means the upflow arrives at a lower temperature as shown in the graph. 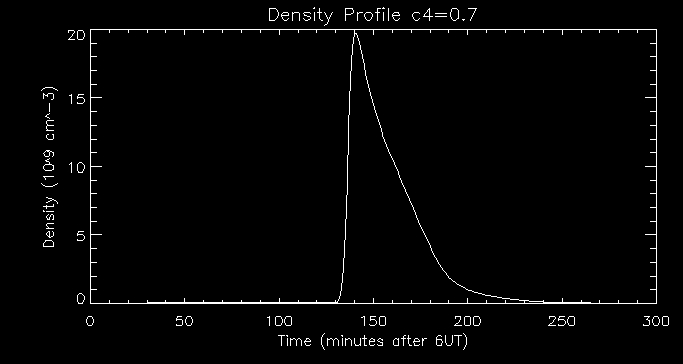Let's now look at the density: Comparing this with our previous density profile we can see that the density peaks at a higher value here - 20 109 cm-3 . Increasing the amount of beam-driven upward flux energises the corona by upward mass flow (evaporation of plasma) which causes the plasma density to reach a higher peak, as shown in the graph. Let's now look at how varying the parameter c1 affects the system. 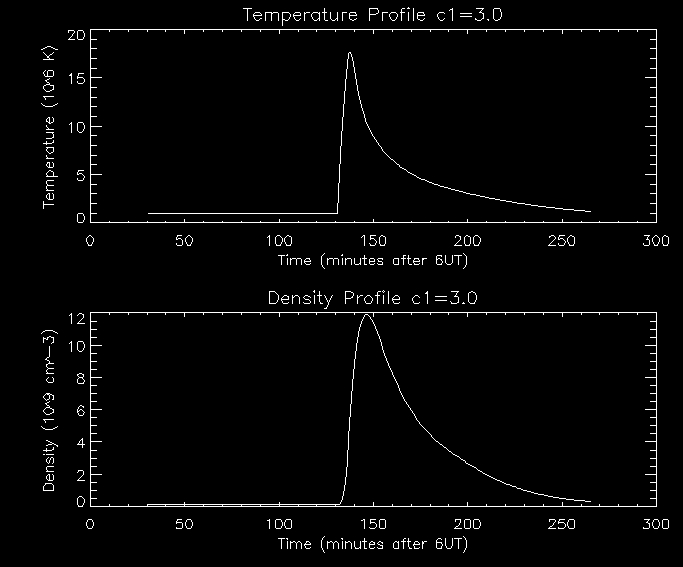We can look at the temperature and density profiles side by side for the case [1,3,0]: In this example we have increased the value of c1 which increases the ratio of radiation loss through the transition region to loss through the corona. This does not affect the flux tube evolution so the peak temperature remains the same. It does however affect the cooling decay phase. There will be an increase in the downflow (coronal condensation) which the flux tube to cool down more slowly.  I am not yet sure of why the flux tube cools down more slowly. The imbalance between conduction from above and radiation loss through the transition region will be decreased so there will a reduced upflow of mass and hence a reduced peak density as illustrated by the graph above. Lastly I will increase the value of c0, while leaving the other two parameters as they were i.e. 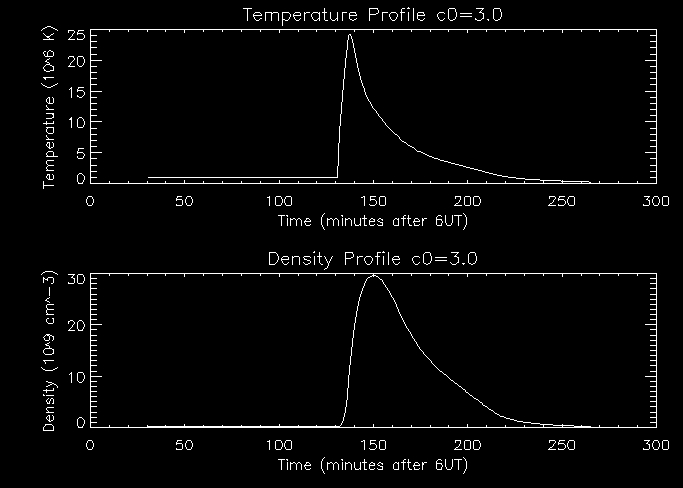[3.0,1.0,0.0]: When we increase c0 we increase the total heating flux so the temperature increases as shown in the graph above.  The density also increases with the total heating flux increase, since when the coronal loop is at a higher temperarure more heat will be transferred through thermal conduction, causing a greater imbalance between conduction from above and energy lost, producing a greater mass flow to the coronal loop. Therefore the coronal loop will be much more dense. I will next look into how calculate the pressure. I modified the EBTEL procedure so I could calculate P =2nkT, where k is the Boltzman constant. 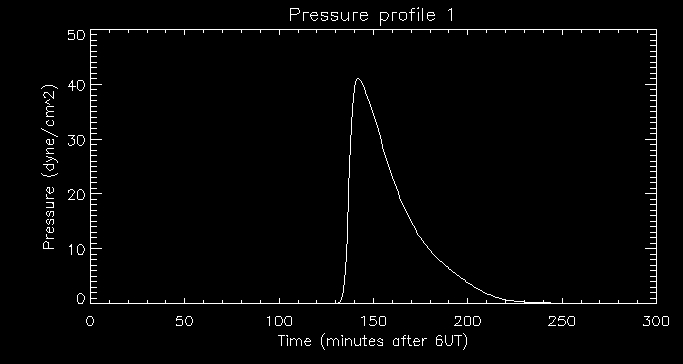Here is an example of a pressure profile of the brightest pixel: As we can see the pressure also peaks around 140 minutes after 6UT as we would expect. Dates: 18th June Today I read through the most recent paper on the model, namely 'Enthalpy Based Thermal Evolution of Loops. II. Improvements to the Model'. This paper focuses on the c1 parameter - the ratio of the transition region (TR) to coronal radiative losses. Two pieces of Physics are added in to develop new models for this parameter: gravitational stratification and a physically motivated approach to radiative cooling. By comparison with a 1D Hydrad model and looking at each modification individually it becomes clear that both modifications are essential. The inclusion of gravity does not affect the TR radiation since it is driven by downward heat flux however the coronal radiation falls due to stratification. c1 increases as the scale height decreases. Overall there were quantifiable improvements using the modified EBTEL model, in particular there was a vast improvement in the density when comparing the new and original versions. Let's look closer at some of the mechanisms that govern the EBTEL model: We divide the loop into coronal and TR parts with the boundary being defined as where thermal conduction changes from a loss to a gain. Whether the flux is into or out of the corona depends on whether the TR is able to radiate the downward heat flux away. If it cannot (essentially Fc > RTR ) material is evaporated into the corona through chromoshperic evaporation (upward mass flow) hence causing the coronal density to increase. If the downward heat flux is not enough to power the TR radiation (Fc < RTR) then there is a downward enthalpy flux (coronal condensation). Last week I was confused by the effect of increasing c1. We can see from looking at the graphs that the corona cools down more slowly. I asked Jiong and found out that this was because the density of the corona had decreased which lowers the amount of coronal radiation. The corona cannot cool down as quickly with less coronal radiation. Dates:19th-20th June The code I need to continue working with the EBTEL model has not arrived yet so Jiong has given me a magnetogram (HMI image) so I can start to experiment with calculating the energy release rate and magnetic reconnection rate per unit reconnected flux. I will look at the magnetic properties of the flaring pixels. The magnetogram only deals with the vertical component of the magnetic field. I first had to coalign with the UV images (AIA data) I used in my introductory IDL project. The images had different pixel scales so I had to use the congrid function to rescale the HMI pixel size then I had to shift the HMI image to align it witth the AIA image. I used the following code: IDL>mmap=rebin(rotmag(500:1953,1900:2867),727,484)<300>(-300) IDL>nmap=congrid(mmap,1454/2.42452,968/2.42452) IDL>ref_uv=dat1600(*,*,50) IDL>setpts,p,ref_uv,nmap IDL>nnmap=shift_interp(nmap,xshift,yshift) The procedure setpts allows you to click on similar points in the two images and outputs the coordinates of these points. I used these coordinates to calculate xshift and yshift, and the function shift_interp shifted the image to coalign it with the AIA image. 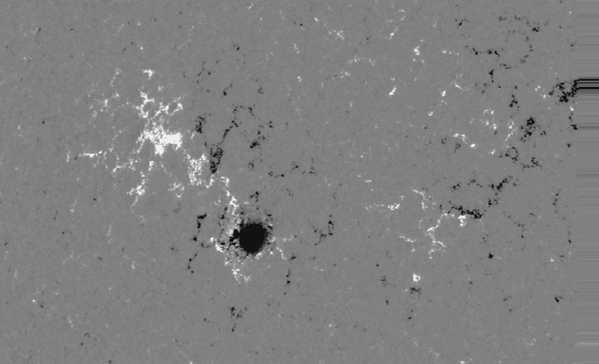Here's the AIA (reference UV) image: and the coaligned magnetogram: The dark shade of the magnetogram display the strong negative field and the white illustrates a strong positive field. 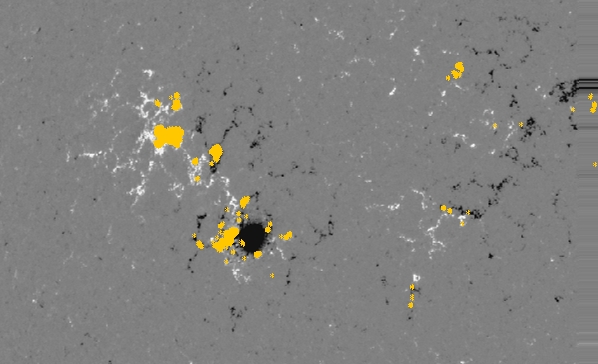We can see the location of the flaring pixels on the magnetogram illustrated below: Now I want to look into some of the magnetic properties of the flaring pixels. I calculated the total reconnection flux of the flaring pixels; one positive and one negative. In theory they should be identical but because of assumptions and uncertainties I calculated a positive total reconnection flux of 7.7288173e+20 Mx and a negative total reconnection flux of -2.5749192e+20 Mx.  Next I will calculate the energy per unit flux in all the tubes. Dates:21st June Today I began by calculating the reconnection in each flux tube (simply B*A), and the total energy in each tube (the time integral of the heating rate). Using these values I then managed to calculate the energy per unit reconnection flux in each of the 600 tubes. I found values ranging from 4.41300e8 to  8.01125e11. I then went on to try and calculate the reconnection rate in the entire flare region. For simplicity I made the assumption that reconnection forming a flux tube takes place at the time when the UV emission of each particular pixel peaks. I created an array of these times and an array of reconnection flux measured before this time. Using these I will go on to calculate the reconnection rate by taking the time derivative of the reconnection flux array. Dates:22nd June - 26th June Firstly I plotted a histogram of reconnection flux (split into positive and negative parts). As we can see from the histogram the positive and negative reconnection fluxes follow a similar pattern. 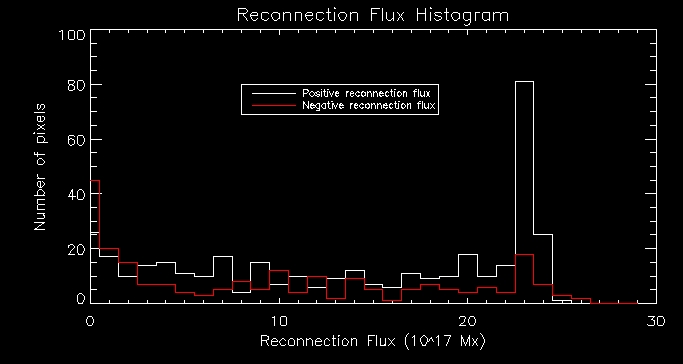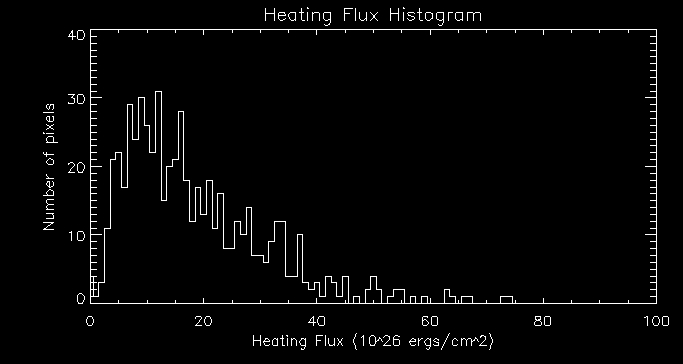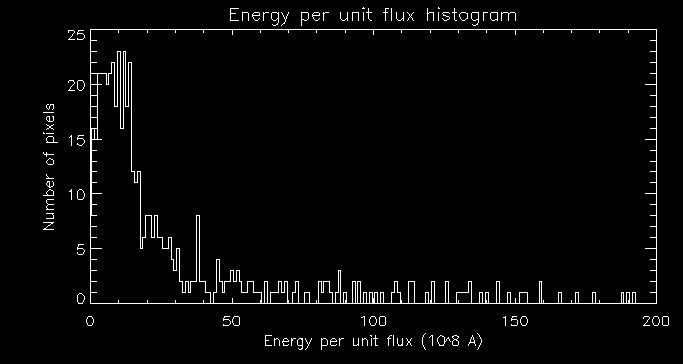Then I plotted a histogram of heating flux: I then plotted a histogram of energy per unit flux: Next I plotted reconnection flux vs time. To make this plot we make the assumption that reconnection forming flux tube takes place at time UV emission of that pixel peaks. The results produce a very nice plot where positive reconnection flux and negative reconnecion flux correlate fairly well. 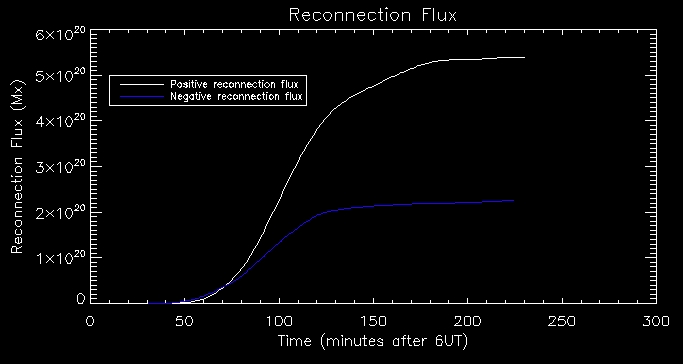Lastly, I plotted reconnection rate vs time, where we see that the positive and negative rates are again fairly correlated for the most part. The reconnection rate continues for a long time backing up that new flux tubes are still forming after the initial impulsive heating. 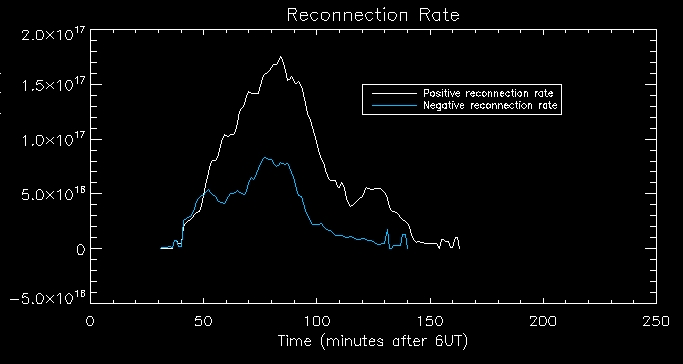(reconnection rate measured in Mx/s - y-axis title cut off) Date: 27th June I will now return to looking at the ebtel model; as I said previously the constant c1 value was unphysical. I will now start to experiment with how best to change this value. c1 scales the loss through the transition region to coronal radiation, which does not make sense physically. We will now try a new approach where we say that the loss through the transition region is proportional to the pressure, by some constant, say, c5 .  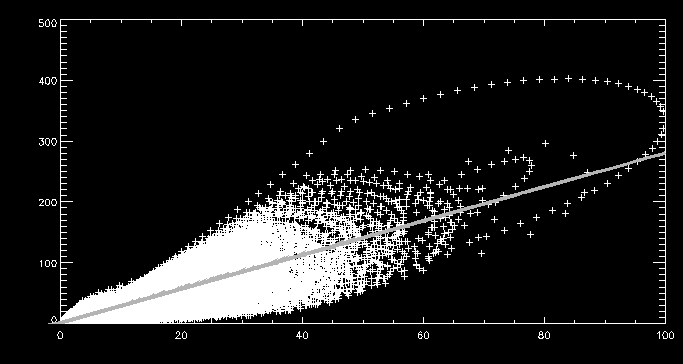To first get an estimate of this constant I produced a scatter plot of the loss through the transition region computed using the EBTEL model against the pressure: In the above scatter plot, pressure is along the x-axis measured in dyne/cm^2 and loss through the transition region is along the y-axis measured in 10^6 ergs/cm^2/s. From this rudimentary approach we get an estimate for c5 of 2.79555e6. Next, I will try a more sophisticated approach where we take the case of static equilibrium. We assume that conduction flux is all radiated away by the transition region and the pressure is uniform from the corona through to the transition region. We can deduce that the differential emission measure, DEM, is proportional to P by some pressure gauge scaler g(T). Using this and the definition of the DEM of a single strand we can deduce that the loss through the transition region is equal to P multiplied by some scalar c5 which we can approximate by the integral of the radiative loss function multiplied by the pressure gauge scaler. Dates: 28th-29th June Using the more sophisticated method we get a value fot c5 of 1.71491e7. 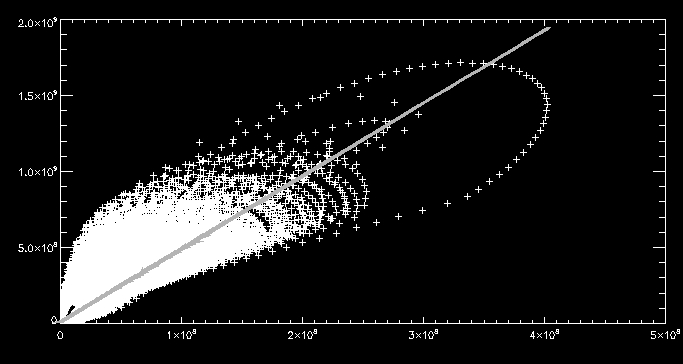We can compute the loss through the transition region estimated through each method and plot them on a scatter plot: Where we have the loss through the transition region computed using the first and second method along the x-axis and y-axis respectively. We discover the losses are different by a factor of 4.79765. To remind ourselves the first method is just the loss through the  transition region computed by multiplying c1 (1.4) by the coronal radiation and the second is the integral of the radiative loss function multiplied by the pressure gauge scaler.  We can now start to look at how varying the loss through the transition region affects the evolution of the plasma. 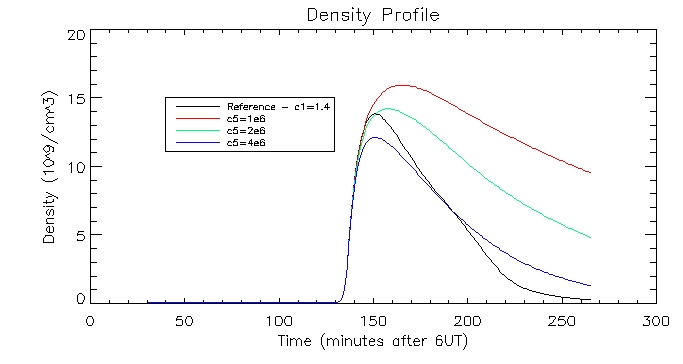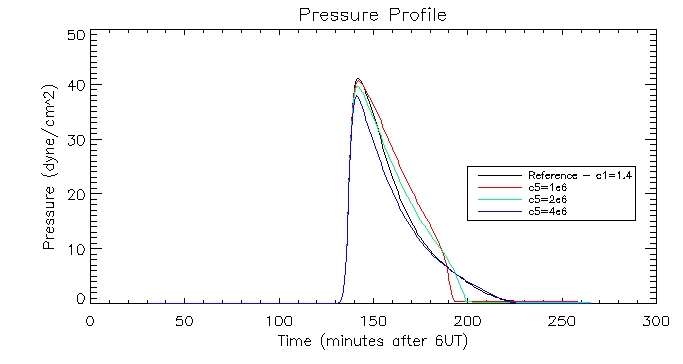Dates: 2nd-3rd July I have produced some plots to display the evolution of the plasma. The white line shows the evolution when the loss through the transition region is scaled with pressure by different values of c5, and the green line depicts the evolution using c1=1.4 as before (scaling with coronal radiation). 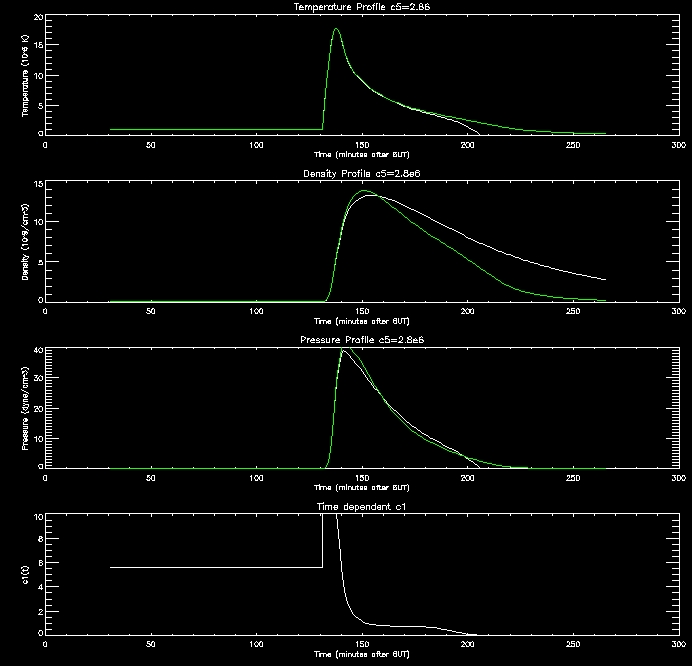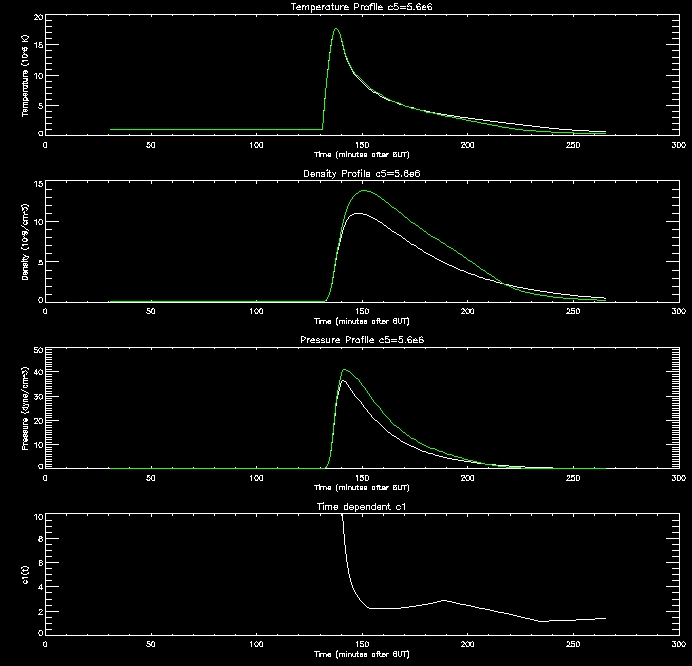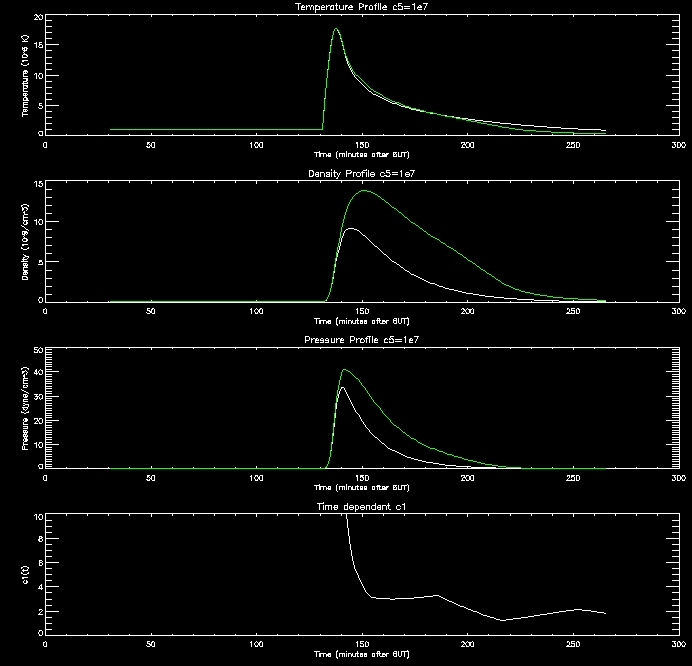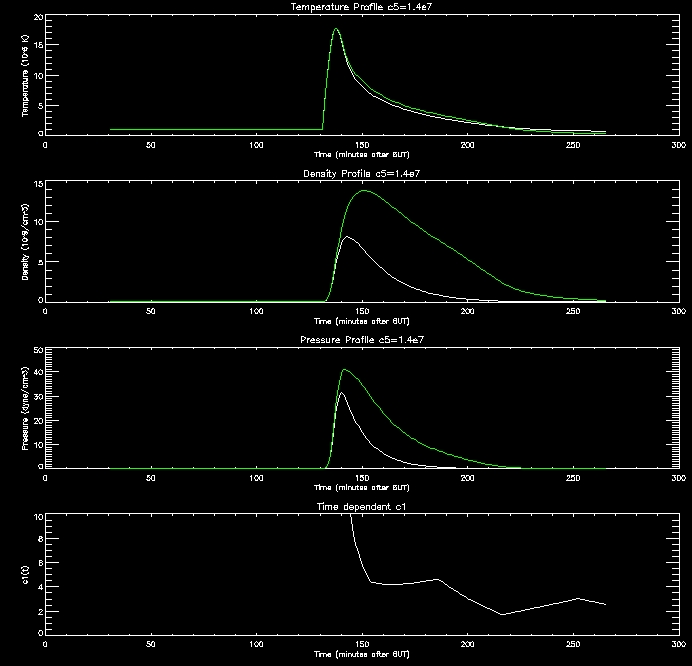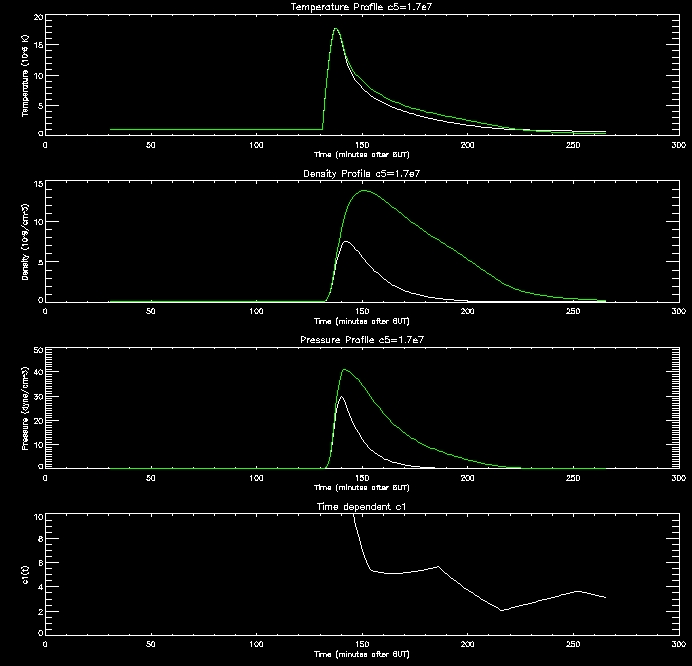These graphs are quite promising. as the c5 value increases (increasing RTR) the density in the corona drops since this creates an imbalance between the conduction flux and loss through the TR which drives the conduction flux lowering the density of the corona.  When the corona is less dense it cools down more slowly, as evidenced by the graphs. Date:  5th-6th July I started to calculate the DEM(T) and realised that I hadn't used cgs units for the Boltzmann constant so was getting the DEM in the wrong order of magnitude.  Having changed the pressure gauge scaler to take this into account we get a different estimate for c5 of 2.04176e6. 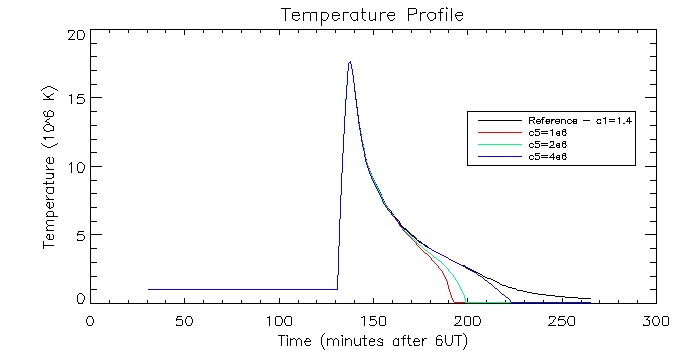I have produced some more graphs to explore this range (i.e. 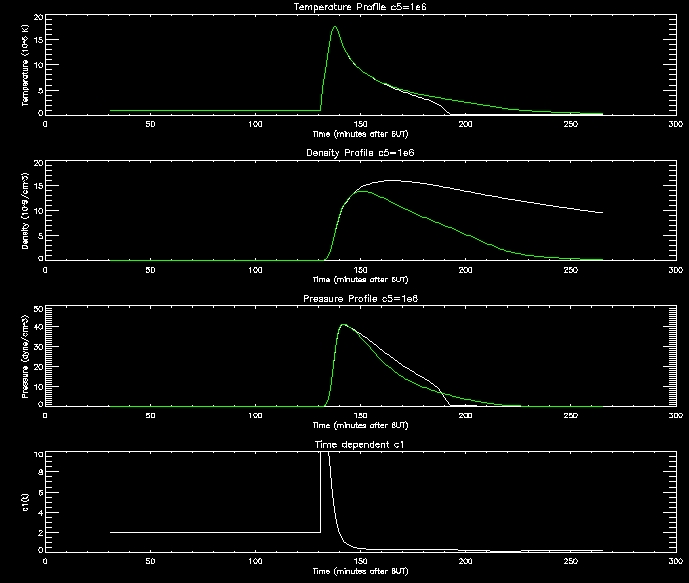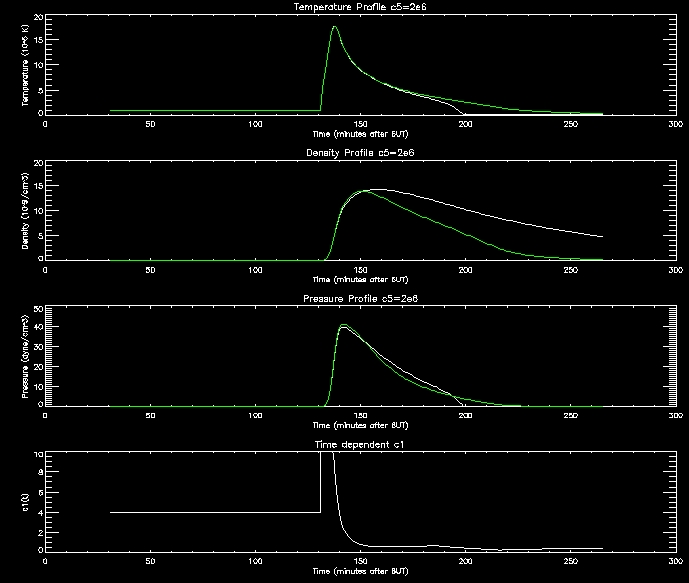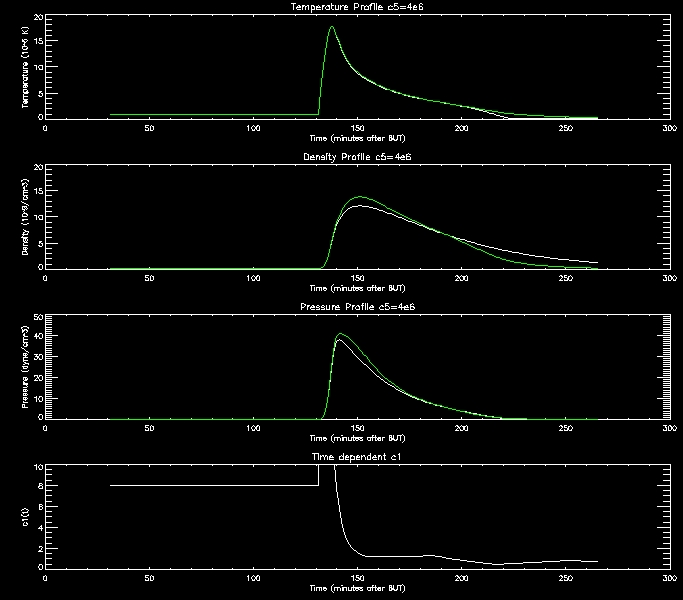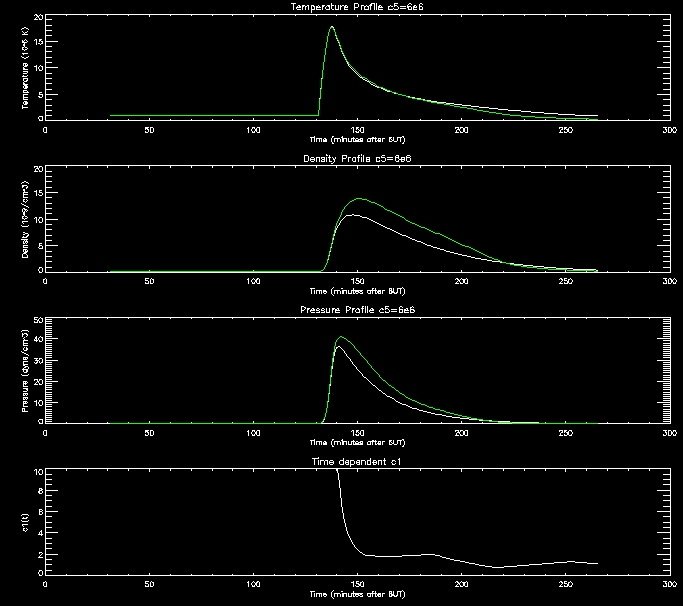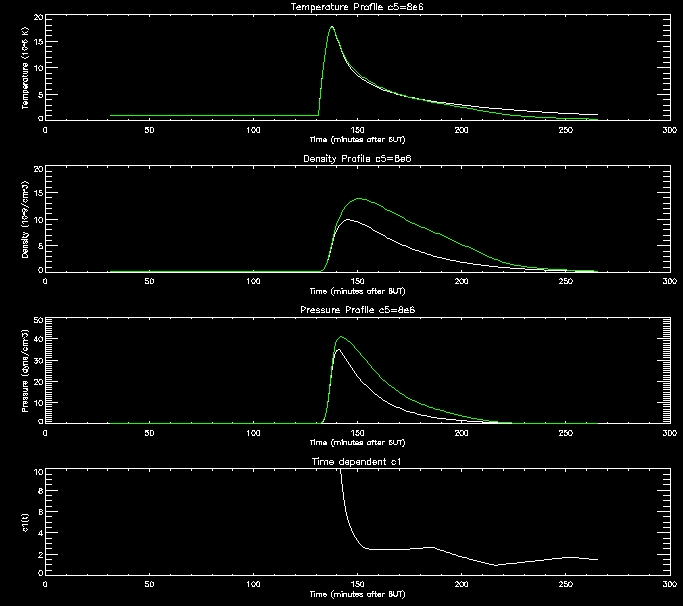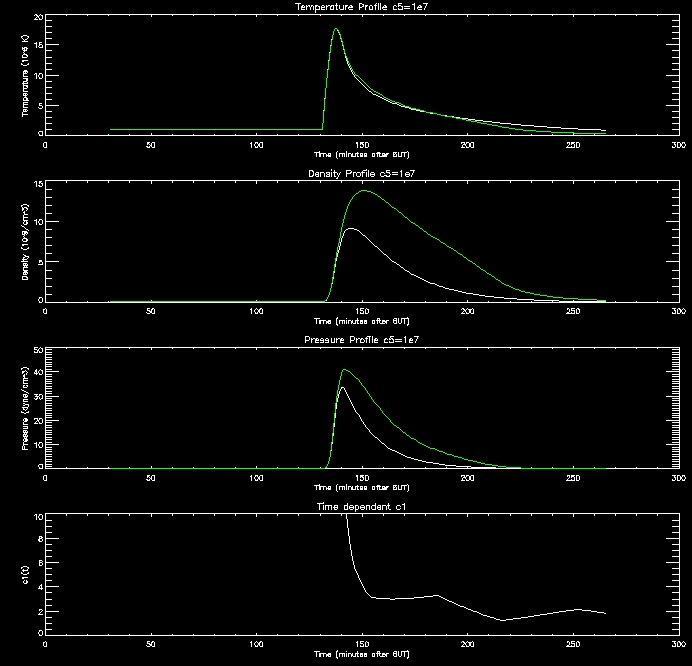c5=[1e6,2e6,4e6,8e6,1e7] For further analysis I will continue to use thses range of values. 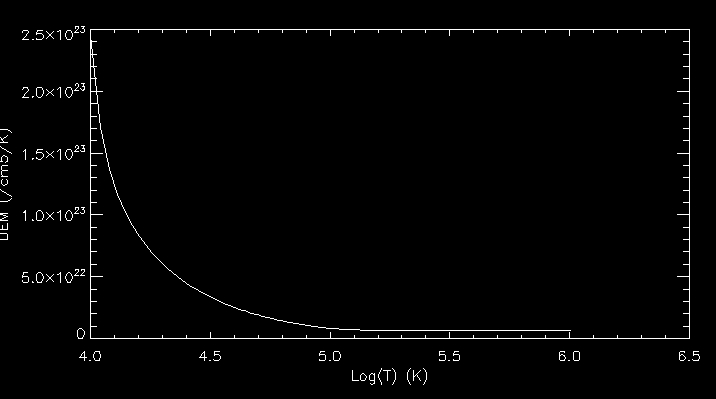I also plotted the DEM against logT: Next I computed the CIV emission for all the values of c5 and plotted them against the observed CIV emission. 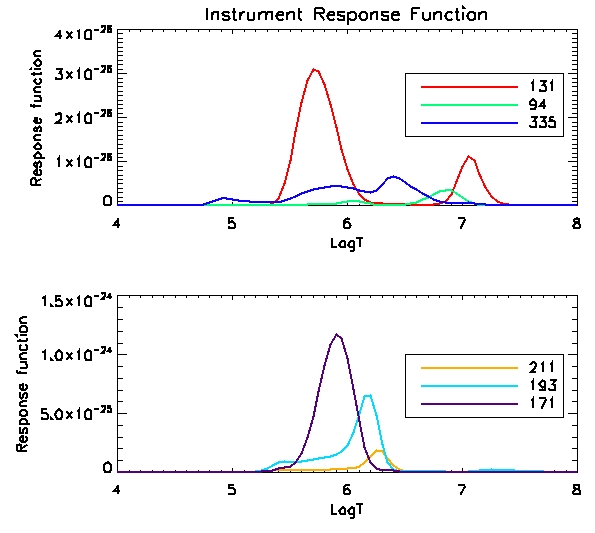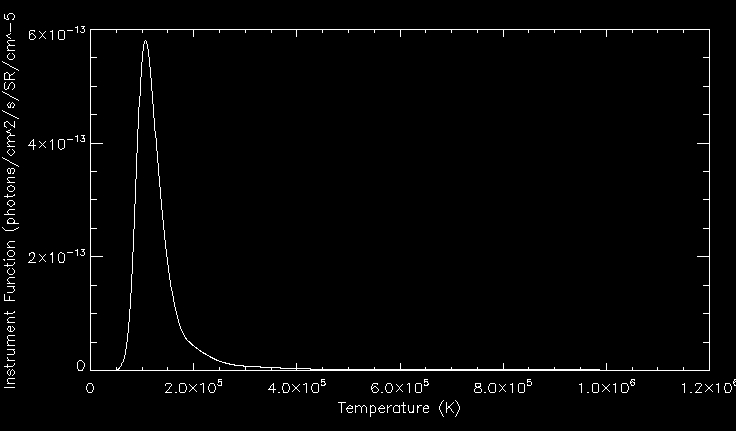We can see the instrument response function against temperature below: We can see the optically thin CIV emission line forming at the transition region temperature of 1e5 K. We calculate the computed carbon IV line by doing the integral int C(T)DEM(T) (scaled with constants - response functions etc). Date: 9th July We can see the observed civ emission is much higher than those computed using the range of c5 values. 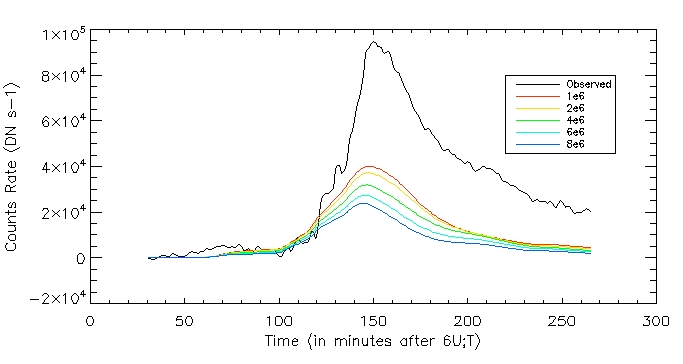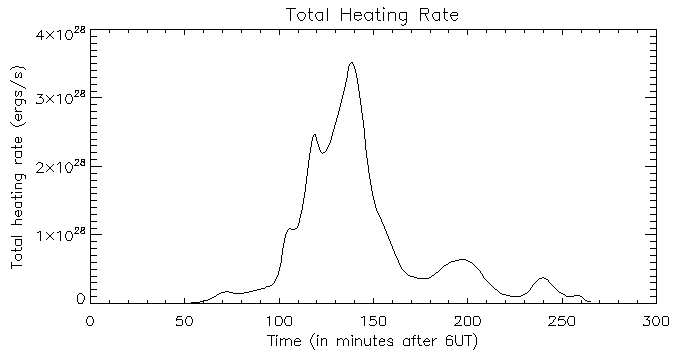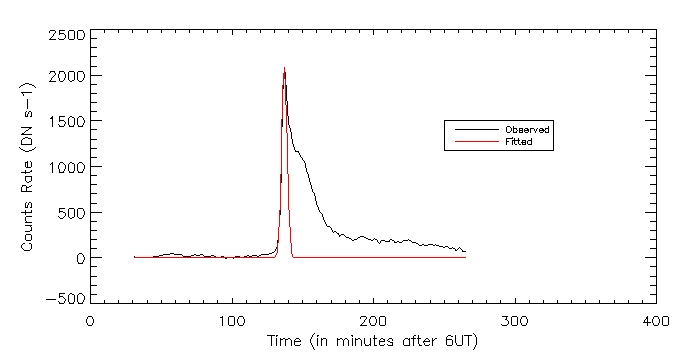Date: 11th July I created a few new plots for my midterm presentation: This is the total inferred heating rate: I also plotted the observed vs fitted heating function for the brightest pixel: I then plotted the temperature, density and pressure profiles for varying c5 values: I also coaligned the AIA 171A image with our AIA 1600A image we have been using so far, plotting the flaring pixels on top: 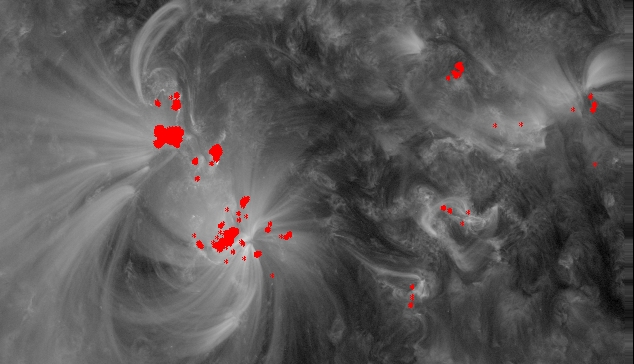I then coaligned the AIA 131 image: and then the AIA 211 image: This image will allow us to compare with our model output later. Date:16th July I aligned the rest of the AIA images. As before the red pixels are the flaring pixels. 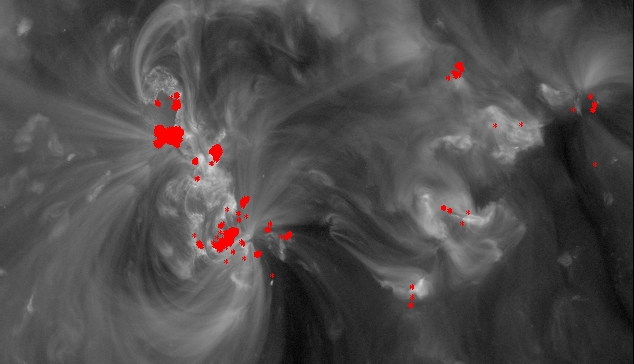The 94 image: The 193 image: The 304 image: 335 image: Date: 17th July I have produced the AIA light curves for the above wavelengths.  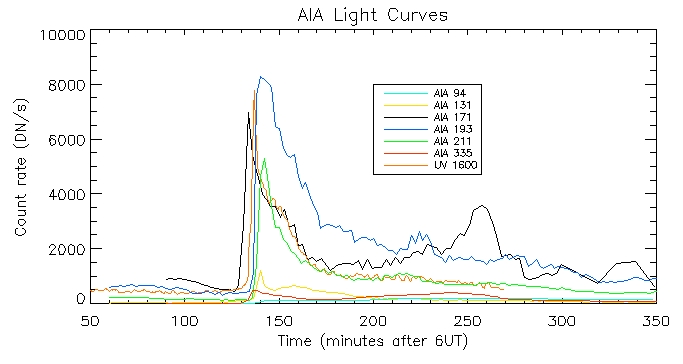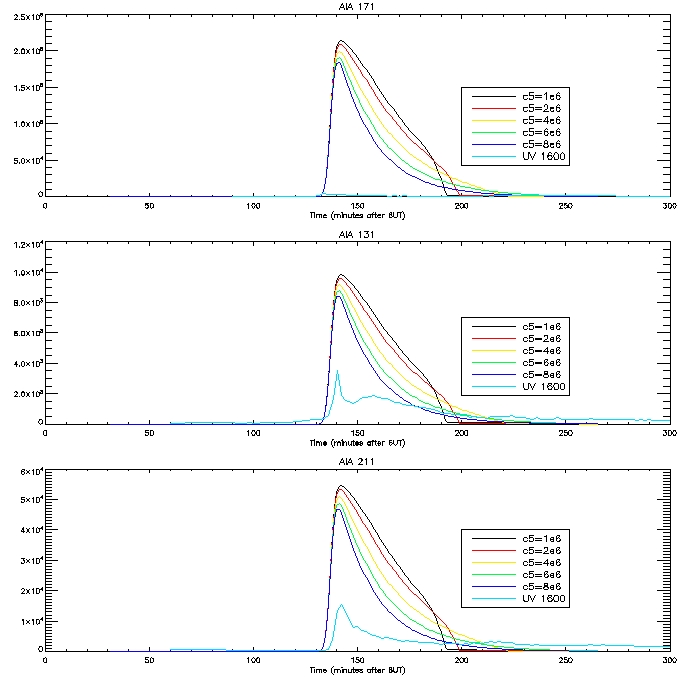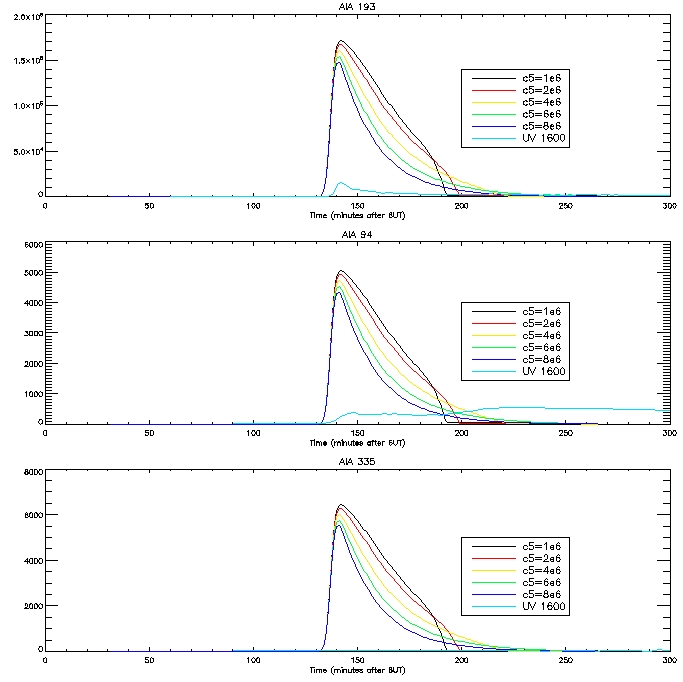This is the light curve of the brightest pixel: Date: 19th July Here are the computed light curves calculated passing our DEM (g(T)*P) through our response function: The results are not very good, especially in the case of 171 and 335. Jiong and I suspect that new loops are forming on the brightened footpoint regions, leading to the second bump in the observed light curves in some cases. The first peak is due to the loop forming which is associated with the footpoint. We have decided that just looking at one particular pixel is not the best approach, it is better rather to look at a bunch of loops in a flare region. 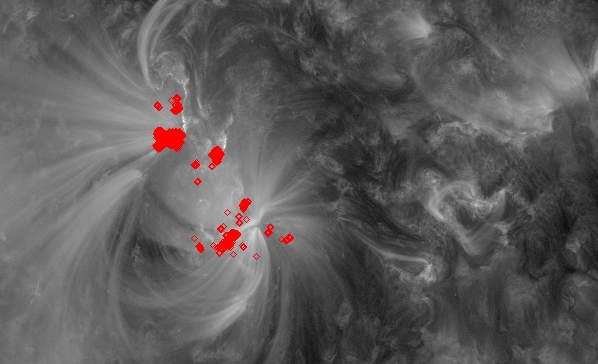Date: 25th July We decided it was best to just look at the flaring regions in the main part of the image and ignore all the trailing flaring regions off to the right. So we are now only looking at 556 flux tubes. 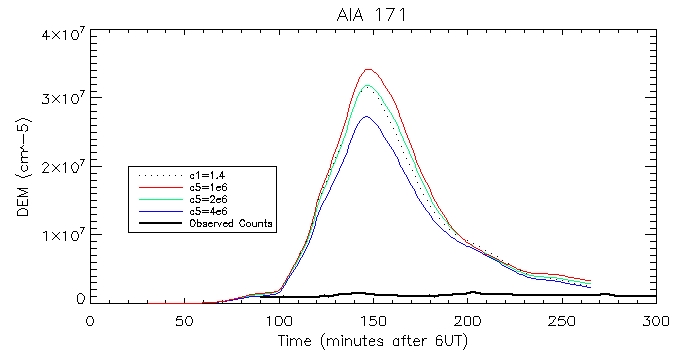We can see an example of this below: Date: 26th -27th July Here we have the computed DEM using the average temperatures and densities across the 556 coronal loops shown above. I did this by summing up n^2(T)*l*R(T). 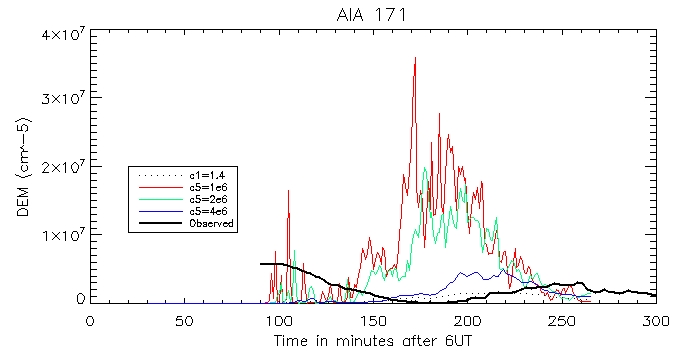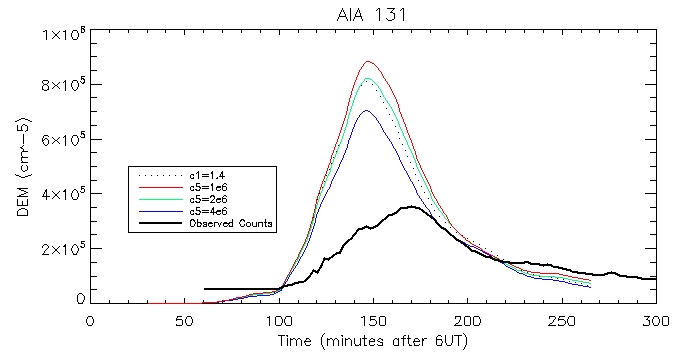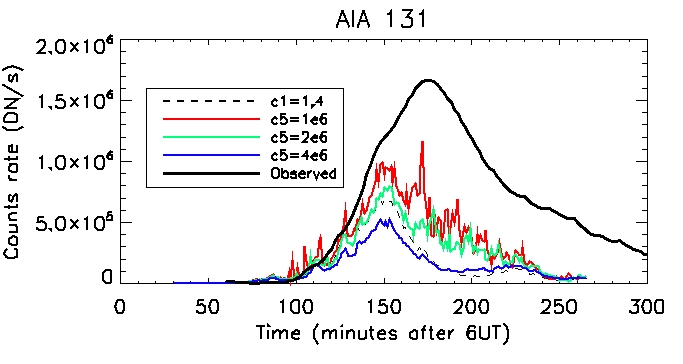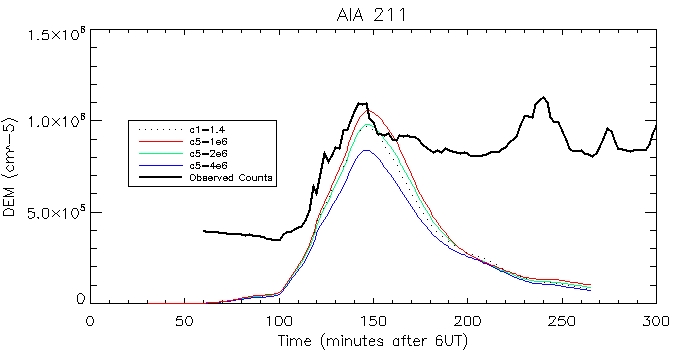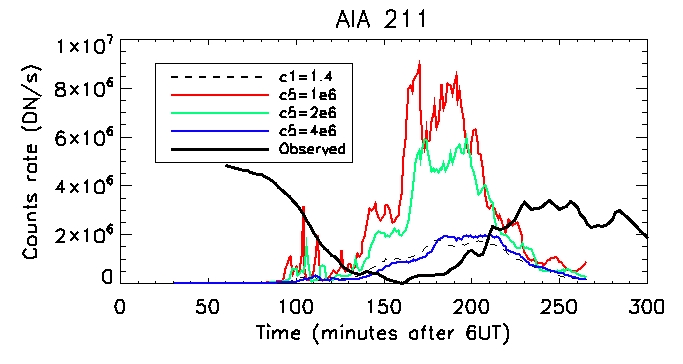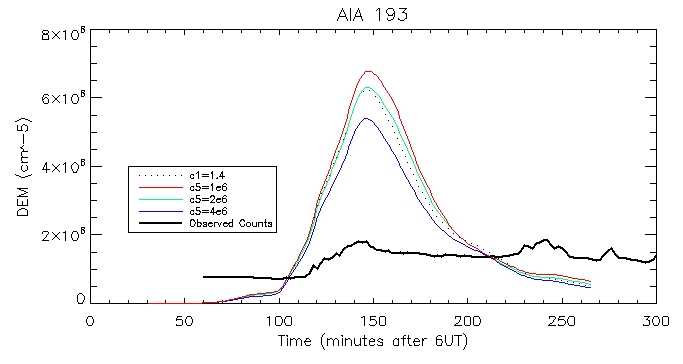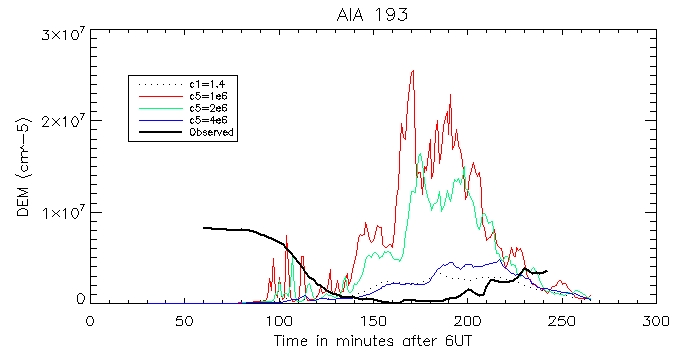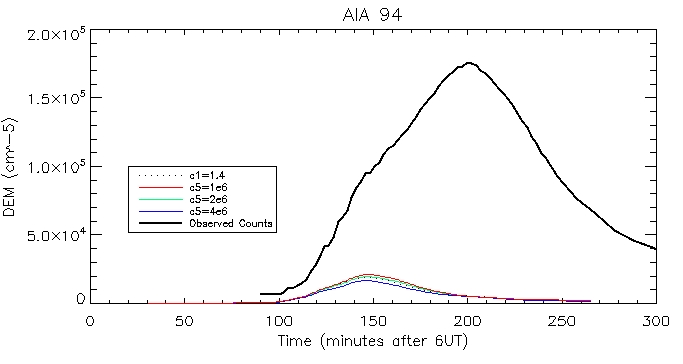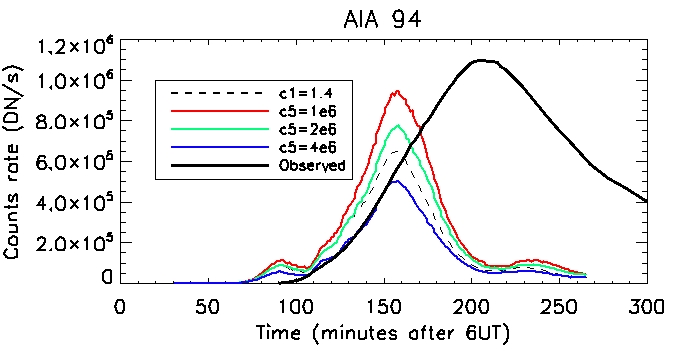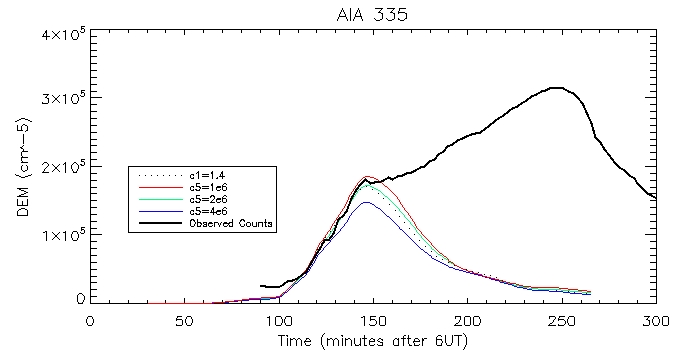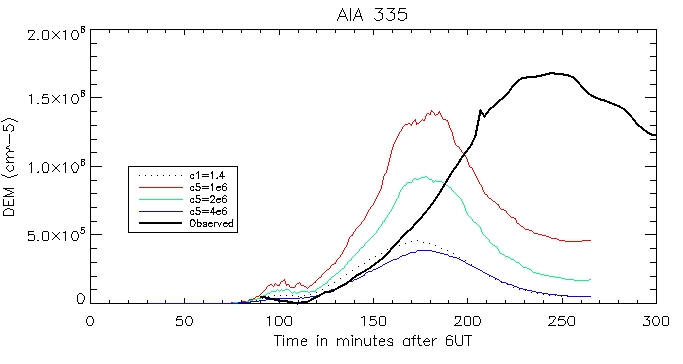And the computed DEM using the footpoints and the pressure-gauge scaler arguement: AIA 131: Coronal: Footpoint: AIA 211: Coronal: Footpoint: 193 Coronal: Footpoint: 94 Corona: Footpoint: 335 Coronal: Footpoint: Date: 30th July I have started to put some graphs together for my final presentation. I will look at the brightest pixel, and another less bright pixel. The temperature, density and pressure profiles I presented for my midterm were of the brightest pixel. 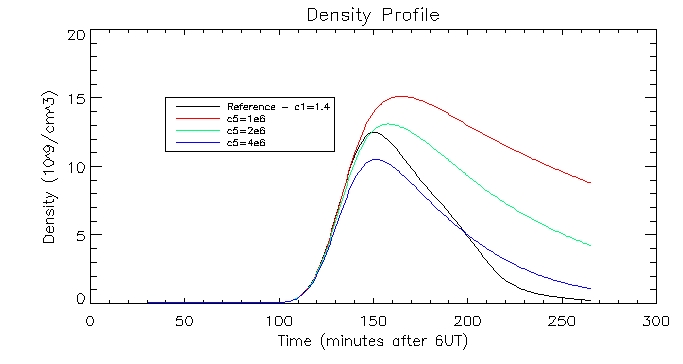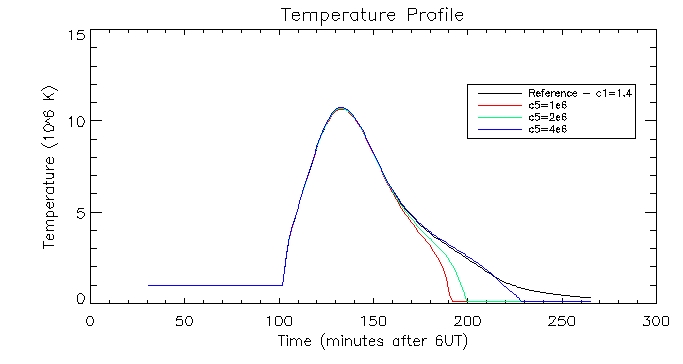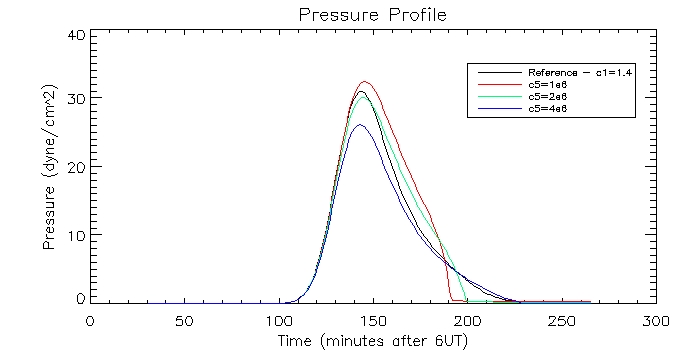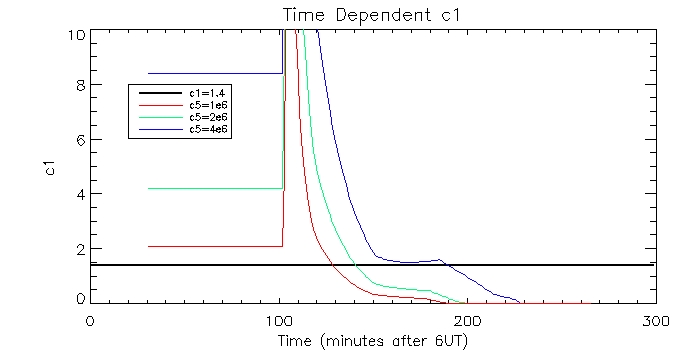Here are the equivalents for the other less bright pixel: I also plotted the time dependent c1s calculating using the pressure gauge scaler method and plotted them against the constant c1 value. 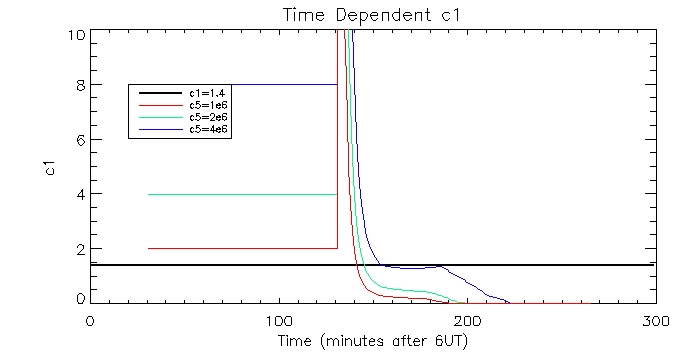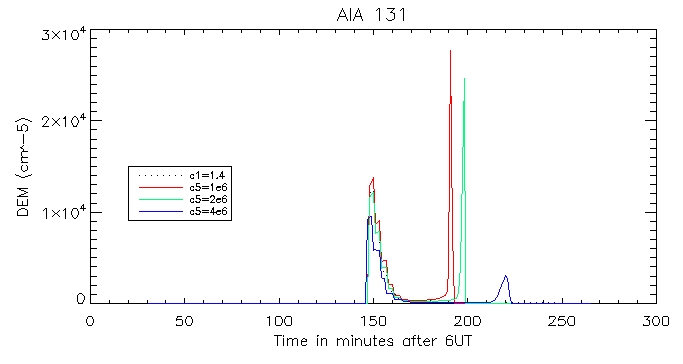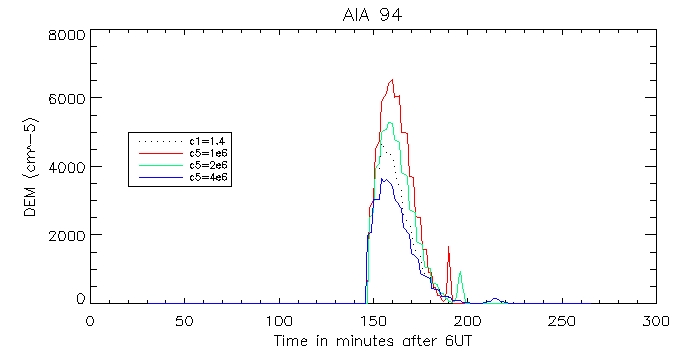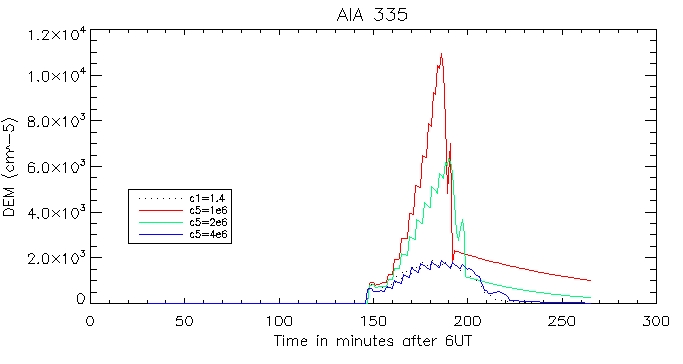Here is the plot of the brightest pixel: And of another less bright pixel: Then the calculated coronal radiation using the coronal DEM for all 6 wavelengths. 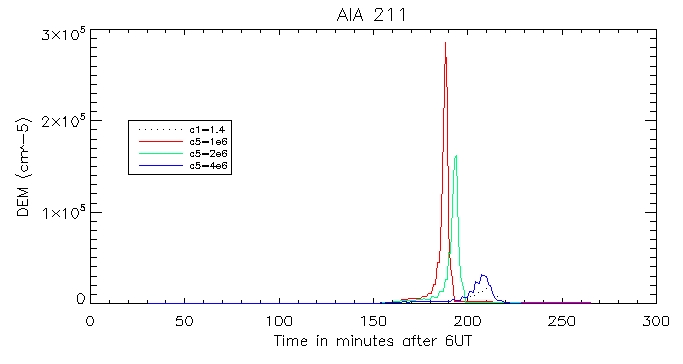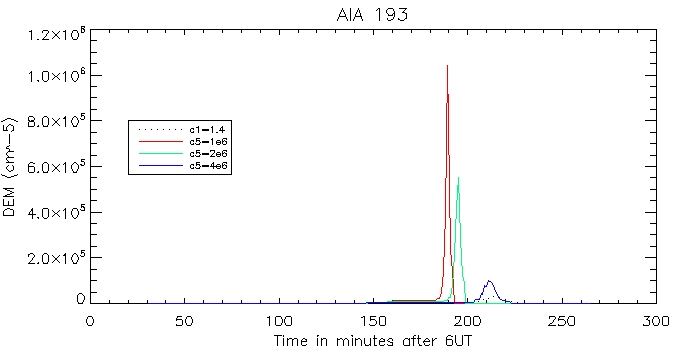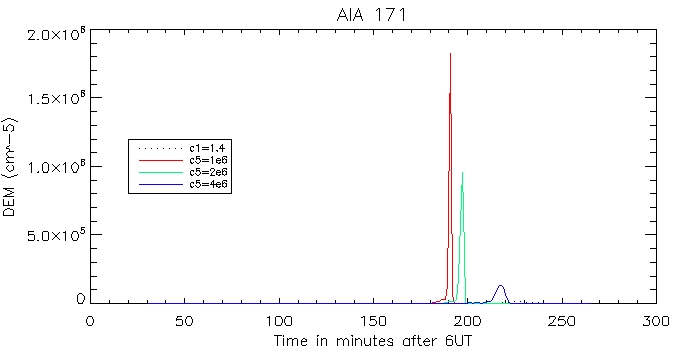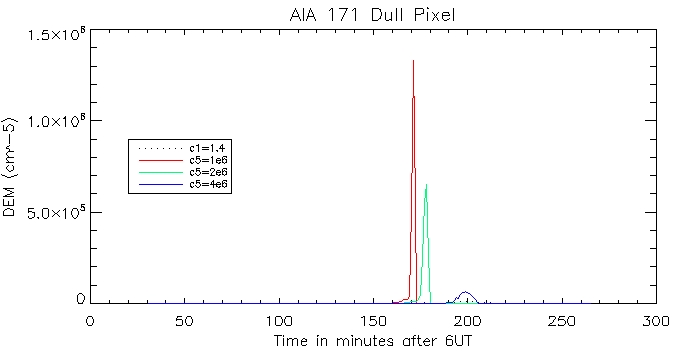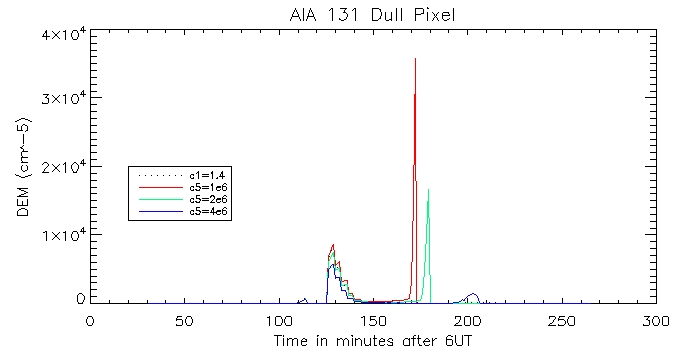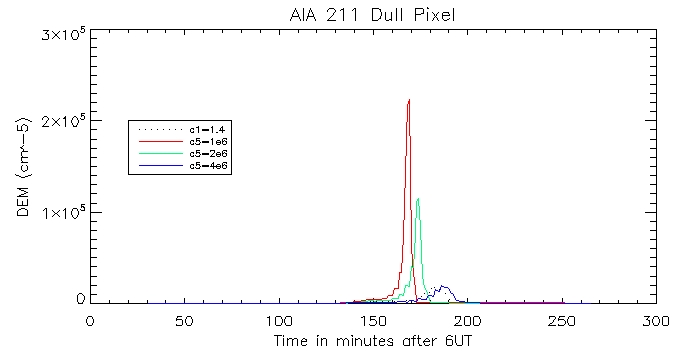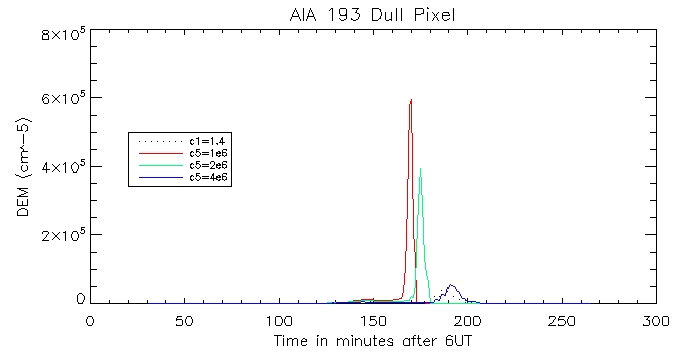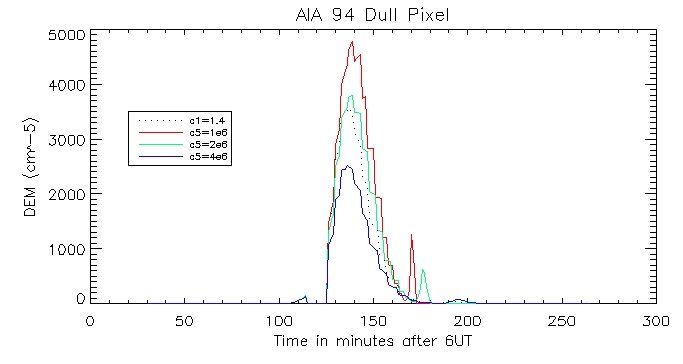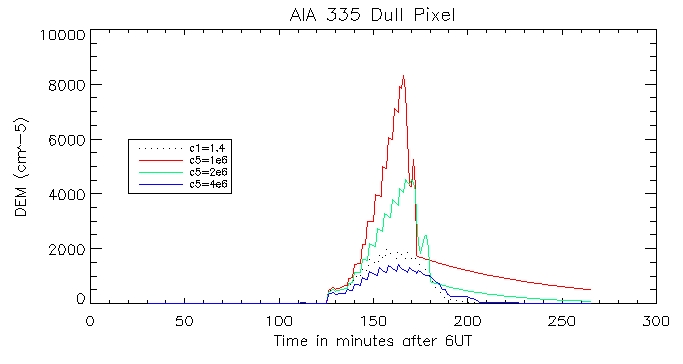Here is that of the brightest pixel: And for the other duller pixel: We can then look at the computed vs calculated footpoint radiation at the brightest pixel, for all 6 wavelengths. 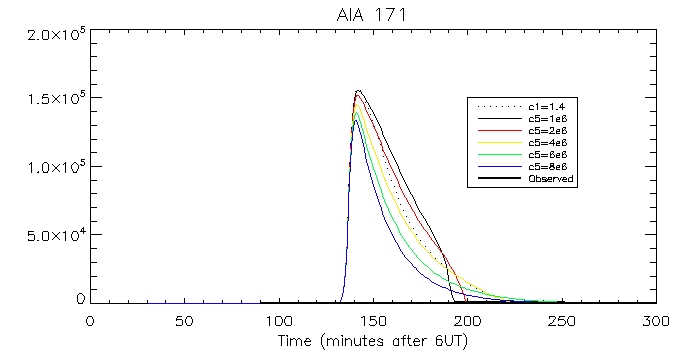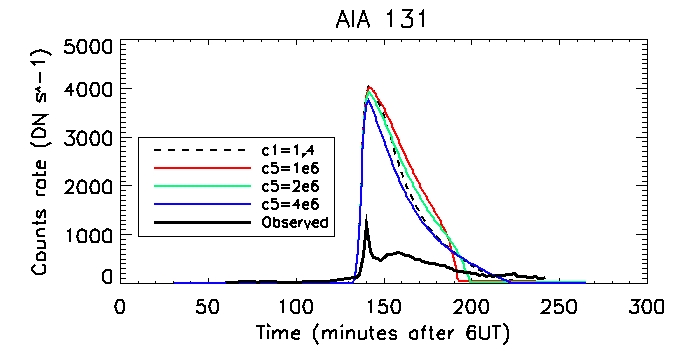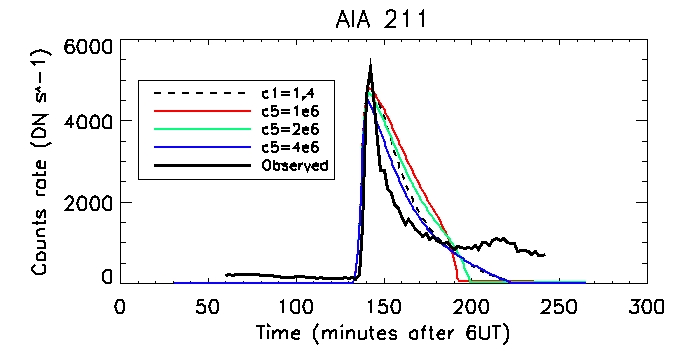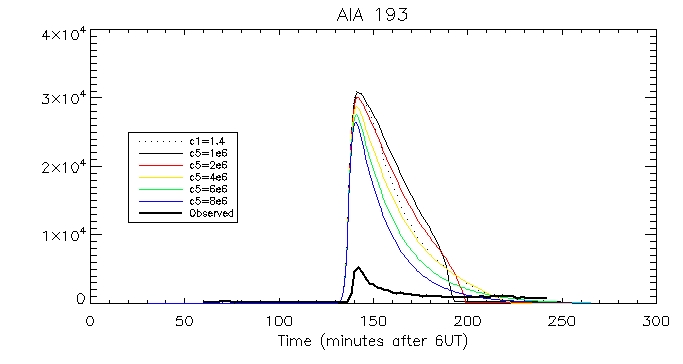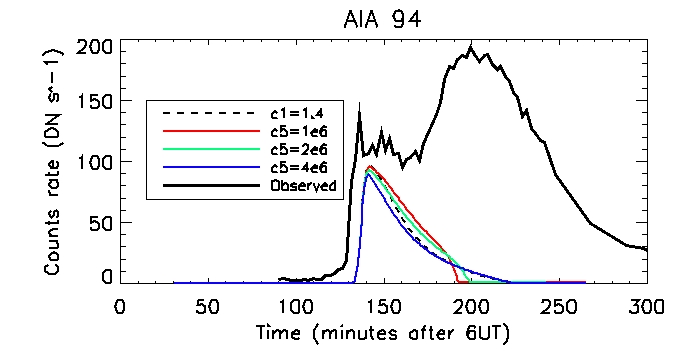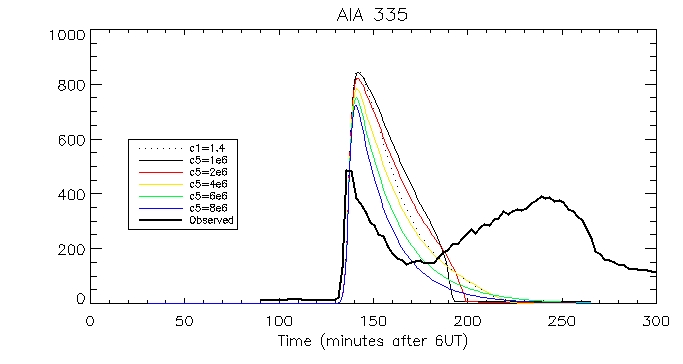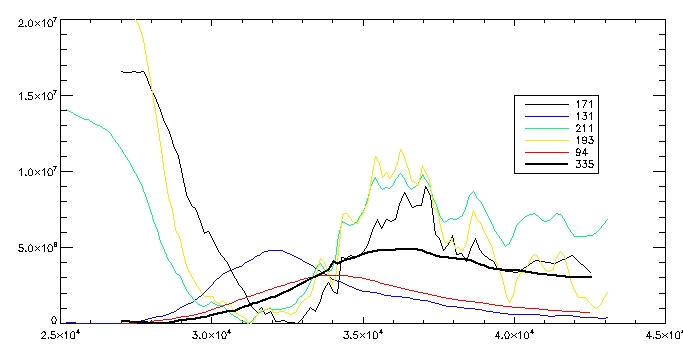This is the observed total coronal radiation over the flare region in all different wavelengths: Date:1st August Today I computed carbon 4 line emission using the pressure gauge scaler method for the range of c5 values. I calculated the DEM then passed it through the CIV contribution function which describes the quantum mechanics of how many CIV photons are produced at a give temperature of temperature range per unit DEM. The units of the contribution function are photons/cm^2/s/SR/cm^-5 (number of photons per second per unit area per solid angle per DEM at a given temperature). We then multiply it by the response function 8.46158e-12*0.003889/2.1. 8.46158e-12 is the solid angle of our pixel, 0.003889 converts photons to DN and is in the units cm^2DN/photon and 2.1 is a calibration factor. Through multiplying by all these constants we get the count rate in DN/s. 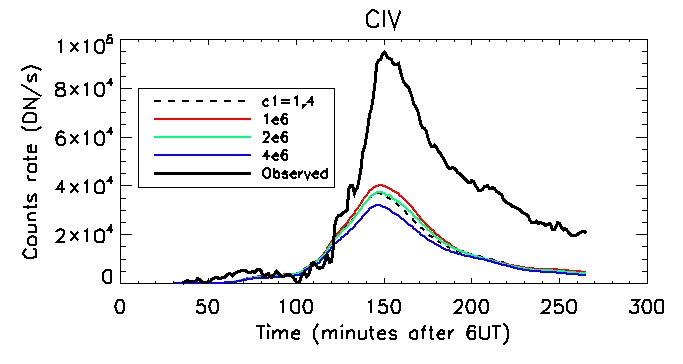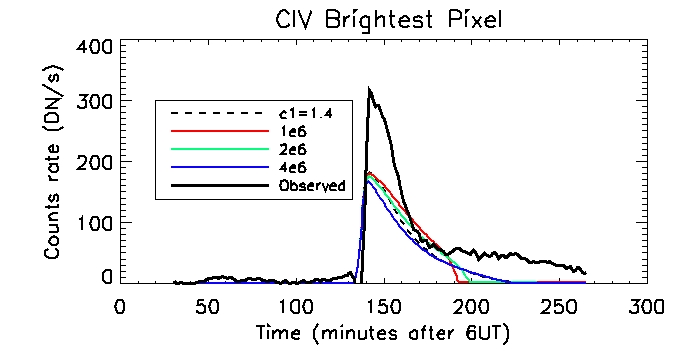And for the single brightest pixel: Here's a plot of the different response functions: