My project this summer has been to develop a set of procedures that will calculate what our model magnetic field looks like, and then compare this with the data we have obtained from the Wind satellite.  By minimizing the value of chi-squared obtained by fitting the data, we have been able to apply the model we have used (see Mathematics section) successfully.

    The program has 6 independent fit parameters, outlined below:
 

•     The initial latitude and longitude, theta₀  and phi₀ , respectively.
•     The 'center time', t₀ ,the time from initial contact with the cloud to the point on the spacecraft's trajectory that is closest to the center of the cloud.
•     Magnetic field magnitude (on cloud axis), B₀ .
•     The radius of the cloud, R₀ .
•     The distance of closest-approach, Y₀ , as a fraction of the cloud radius.

    Our model magnetic field has components in cylindrical coordinates, but our data is in Cartesian GSE coordinates.  Therefore, it was necesary to transform either the data or the model into the coordinate system of the other.  After much trial and error, we decided it would be easier to transform our magnetic field model into Cartesian GSE coordinates.  We did so with the help of a coordinate transformation matrix developed by Dr. Ron Lepping, shown below.

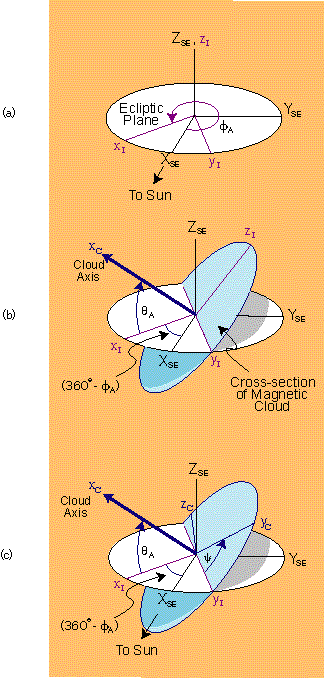
Here we see the 3 rotation steps used to transform from Cartesian GSE coordinates to a new coordinate system where the new x-axis lies along the cloud axis.

The matrix describing the transformation is given as:

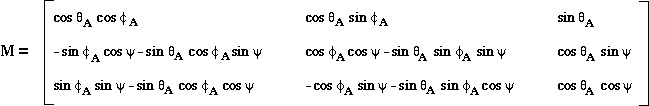where,

(Also, just as a side note, the 'A'-subscripted angles denote the same angles as our '0'-subscripted angles.)

However, since we decided to transform our model magnetic field into Cartesian GSE coordinates, we have utilized the inverse of the matrix, M, above.

    As it turns out, once we transformed coordinate systems, the cross-section of the cloud (as seen by the spacecraft along its trajectory) goes from circular to elliptical.  Now, the geometry we needed to use to adjust our model to include an elliptical cross-section was extraordinarily cumbersome, so I will spare the details.  We needed to adjust the model to calculate the components of the tangential magnetic field at each point along the trajectory, but suffice it to say that after a lot of scribbling on paper, it seemed to work out.

In the program, it was necesary to make a call to AMOEBA, a function built in to IDL that performs a multi-dimensional minimization of a function via the Downhill Simplex Method (for a brief introduction to the DSM, click here).  We wish to minimize the function that calculates our chi-squared, which requires finding a global minimum.  However, AMOEBA can be easily mislead, and sometimes it will converge only a local minimum.  Therefore, in some cases, we had to try several different simplexes (sets of initial values) before arriving at our globally minimized chi-squared.

Using the accepted start- and stop-times for several magnetic clouds, found here, we were able to download the data from several magnetic cloud events, applying the fitting programs to each set of data.  In the next section, we will see just what kind of results we have obtained over the course of the last 10 weeks.