Frozen-in Aproximation - AMJ - REU2003

Frozen-in Aproximation

The equation which governs the behavior of magnetic fields in a plasma is the induction equation:

$\begin{displaymath}{\partial {\bf B}\over\partial t}=\nabla \times ({\bf v\times B })+ \lambda \nabla^2 {\bf B}\end{displaymath}$

In order to know which of the right side terms dominates the ratio between the two can be found which is aproximately:

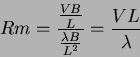
$\begin{displaymath}Rm= {{{VB}\over L}\over{{\lambda B}\over L^2}} = {VL\over \lambda}\end{displaymath}$

which if greater than one will mean that the first term rules the behavior of the magnetic field so the induction equation can be written as:

$\begin{displaymath}{\partial {\bf B}\over\partial t}=\nabla \times ({\bf v\times B })\end{displaymath}$

Which has the same form of the vorticity equation, so in analogy with the Kelvin's vorticity theorem we can show that the magnetic field satisfies:

$\begin{displaymath}{d\over dt}\int_{S}{\bf B}\cdot d{\bf S}=0\end{displaymath}$

Which means that the magnetic field remains "frozen" and moves with the plasma material.

Home