Week 1
Settling In
I could get used to the kind of scenery that Bozeman has to offer. The air fresh, the mountains are tall, and the people I've met thus far are all incredible. The introduction to Filament wasn't too bad as I've had previous experience working on remote servers running on Unix, and the Python tutorials were a good refresh for all the code I'll be writing. I thoroughly enjoy the amount of walking and bike riding I get to do. It's great to see a community that's so active. Over the weekend, we took a hike to the 'M', walked a little stretch of the Gallatin river, and I was able to go out with a friend to Buffalo Jump State Park and Three Forks (where the Gallatin, Madison, and Jefferson rivers meet to form the head of the mighty Missouri).
Aside from all the fun and adventure, I had my first meeting with Dr. Hang Yu on Wednesday. We discussed the main publication we'd be refrencing, and talked about the differential equations I'll be evolving to model our binary white-dwarf(WD) systems. I did a few preliminary calculations of values with physical importance to the project. Week two came really fast.




Week 2
Physical Intuitions and Initial Code
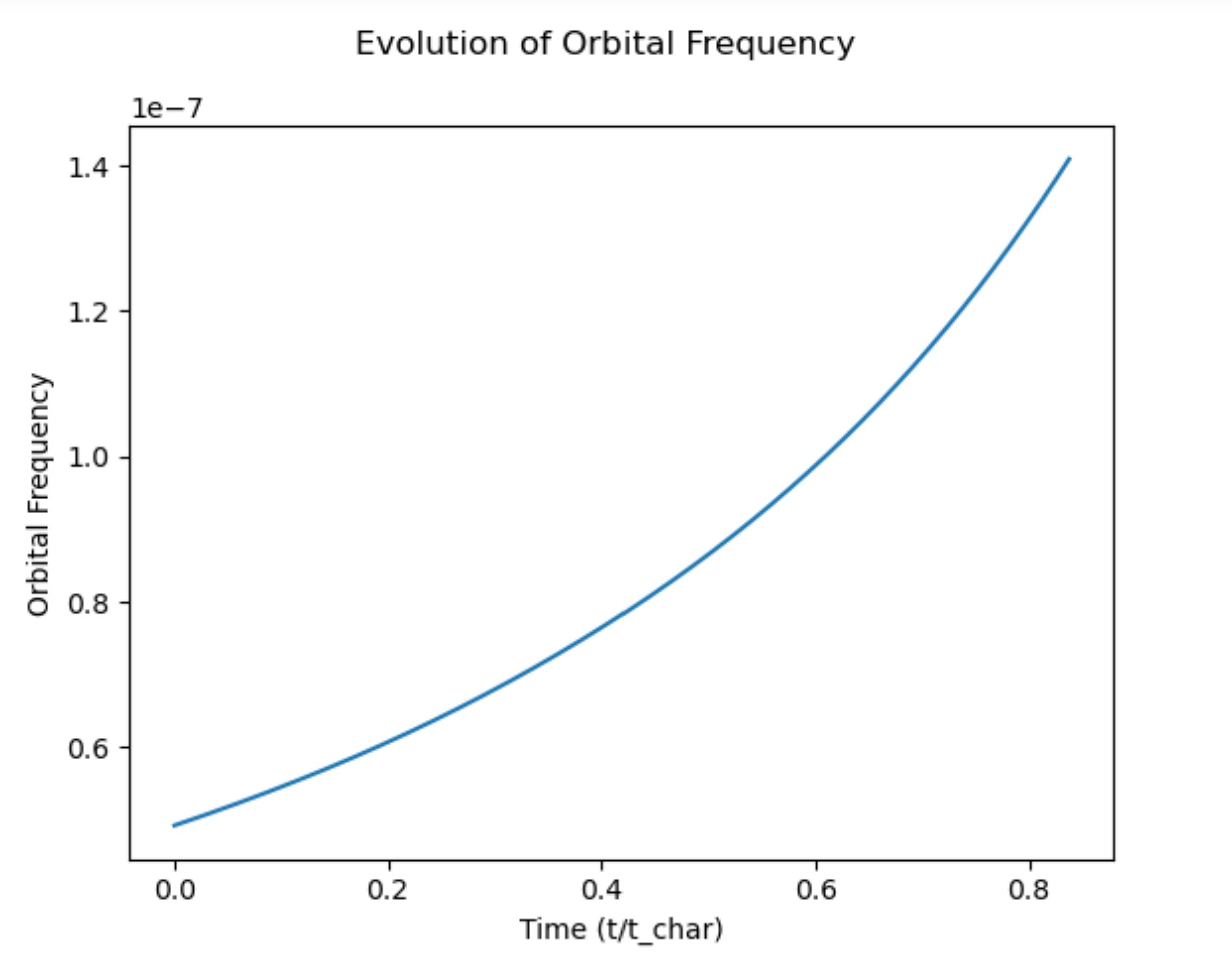
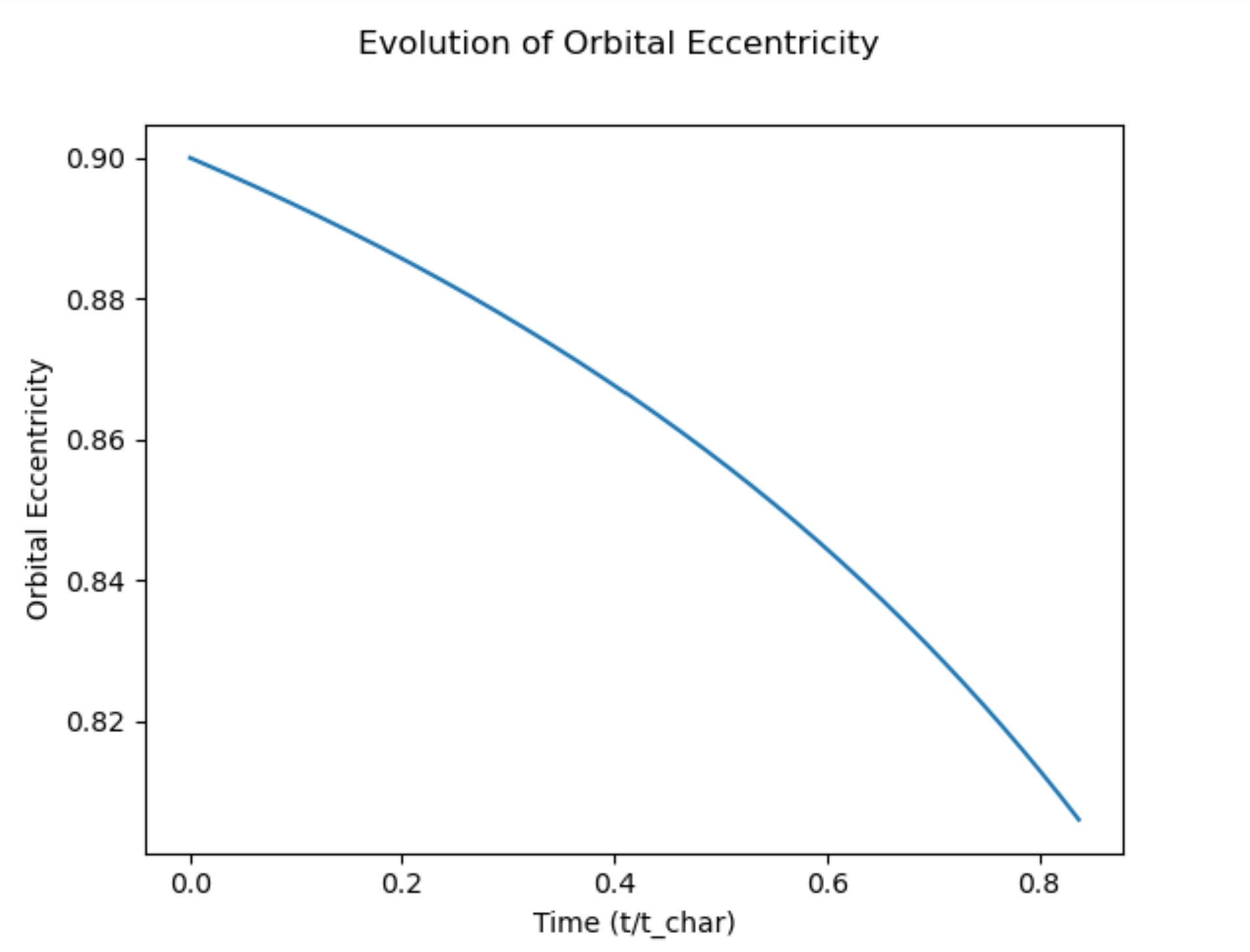
This week I really dove into writing some code, but it's only the beginning. There is so much more to come. Dr. Hang Yu has really stressed the importance of a good physical intuition of these systems as a measure we can take to ensure our results are making sense. We start by only evolving Eqs. 2 and Eqn. 4 from the figure above. These equations, representing the rate of change of the orbital frequency and eccentricity, only depend upon one another and solving these two coupled ODEs is quite simple. But wait, they have SI units, no not even that, they have units in general! We can't have this. Our computers don't like working on numbers with units that in turn result in values with large orders of magnitude. So before we evolved them, we must first figure out how to get them into a unitless form. In doing so, we can derive a characteristic timescale that tells us a lot about the way the system evolves. Once that was sorted out, we needed to figure out if we shoul keep the Post-Newtonian(PN) terms on the end of the equations. These take into account small relativistic effects that are really only present in systems containing large black holes. After a little math, I determined that the PN terms are only contributing a miniscule fraction of the main body of the equation when we consider smaller systems like a binary WD pair. That being said, we are not keeping the PN terms. Finally, I had to make some quick approximations of what our results should be before actually performing the numerical integration and plotting our results. This all looks good!



This friday, we each gave a two week update presentation.